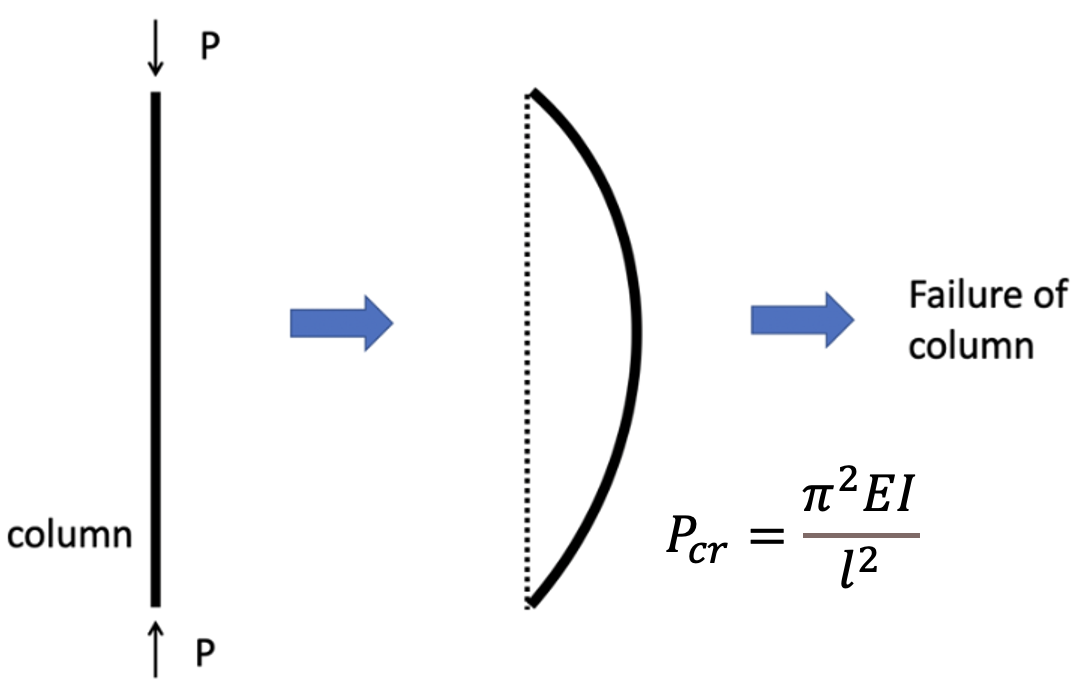
ដូចបង្ហាញក្នុងរូបភាពទី១ យើងនឹងសិក្សាករណីសរសរមួយស្ថិតនៅក្រោមបន្ទុកខ្ទប់(compressive load)។ ពេលដែលបន្ទុកកើនឡើង កំណោងនិងស្ត្រេននៃសរសរក៏កើនឡើងដែរ។ ដោយសារតែភាពតាន់(flexural stiffness)របស់វា សរសរអាចធុនជាមួយកម្លាំងបានមួយរយៈ។ ប៉ុន្តែពេលបន្ទុកកើនឡើងដល់កម្រិតមួយ កំណោងធំខ្លាំងរហូតទាល់តែសរសរស្ទើរតែបាត់បង់ភាពតាន់ទាំងស្រុង។ ហើយពេលដែលភាពតាន់លេងមានប្រសិទ្ធភាព សរសរនឹងបាក់ភា្លមៗ។ បាតុភូតនេះហៅថាbuckling ហើយបន្ទុកអតិបរិមាដែលសរសរអាចទ្របានមុនពេលបាក់ហៅថាបន្ទុក buckling។
ក្នុងឆ្នាំ១៧៥៧គណិតវិទូស្វីសលោក លេអូណាដ៍ អឺលែ (Leonard Euler) បានសិក្សាលើបាតុភូតbuckling ហើយបានកំណត់បន្ទុក buckling ដោយជោគជ័យ។ ចាប់តាំងពីពេលនោះមកបន្ទុកbucklingត្រូវបានគេស្គាល់ថាបន្ទុកអឺលែ(Euler’s load, Euler’s critical load)។ ខាងក្រោមនេះគឺជារបៀបនៃការគណនាបន្ទុកអឺលែ។
ការសន្មត:
១. បន្ទុក P កើនយឺតៗដោយល្បឿនថេរ ហើយចុងសងខាងនៃសរសរគឺ hinged end ។
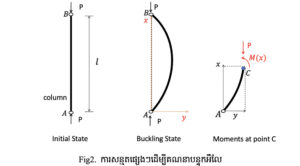
២. សន្មតកូអរដោណេ (Axy) (រូបភាពទី២) ដែល x កាត់តាមផ្ទិតម៉ាស(center of gravity, centroid) នៃសរសរ ហើយ y(x) គឺជាកំណោងត្រង់ x ។
៣. សន្មតថាbucklingកើតឡើងត្រង់ C(x,y)
ដោយសារចុងសងខាងគ្មានកម្លាំងប្រតិកម្ម នោះគ្មានshear stress ចំពោះគ្រប់មុខកាត់ទាំងអស់។ ដូចនេះកម្លាំងក្នុង(stress)មានតែម៉ូម៉ង់តែមួយគត់ដូចរូបខាងស្តាំ។
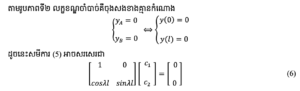
ចម្លើយងាយនៃសមីការ (6) គឺc1 = c2 = 0 ដែលមានន័យថាគ្មានឥទ្ធិពលនៃបន្ទុក ឬថាសរសរស្ថិតនៅត្រង់ដដែល។ យើងមិនអាចទាញយកបន្ទុក buckling បានទេក្នុងករណីនេះ។ ដូចនេះយ៉ាងហោចណាស់មួយក្នុងចំណោម c1, c2 ត្រូវតែជាចំនួនពិតខុសពីសូន្យ។ ដើម្បីបានលទ្ធផលបែបនេះដេទេមីណង់នៃម៉ាទ្រីសមេគុណត្រូវតែស្មើសូន្យ ហើយលក្ខខណ្ឌនេះហៅថាលក្ខខណ្ឌ buckling (សមីការ (7) )។
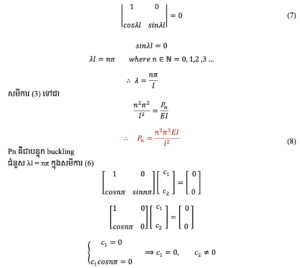
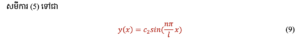
សមីការនេះបញ្ហាញពីម៉ូត(ទ្រង់ទាយ)នៃ buckling របស់សរសរ។ ម៉ូតនៃbuckling និងបន្ទុក buckling អាស្រ័យលើតម្លៃនៃ n ដូចបង្ហាញក្នុងរូបភាពទី៣។ ករណី n = 0 គឺជាករណីគ្មាន buckling។ ក្នុងទ្រឹស្តីគណិតវិទ្យាម៉ូតមួយណាក៏អាចកើតឡើងដែរ។ ក្នុងការអនុវត្តជាក់ស្តែង ពិសេសចំពោះបន្ទុកដែលកើនឡើងយឺតៗដោយល្បឿនថេរដូចការសន្មតខាងដើម មានតែម៉ូតទី១ប៉ុណ្ណោះដែលកើតឡើង។ ដូចនេះបន្ទុកbuckling ឬបន្ទុកអឺលែត្រូវបានកំណត់ដោយ
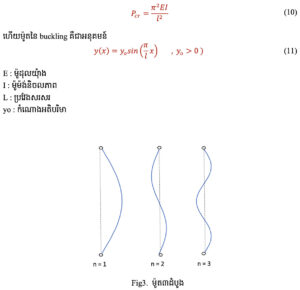
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
