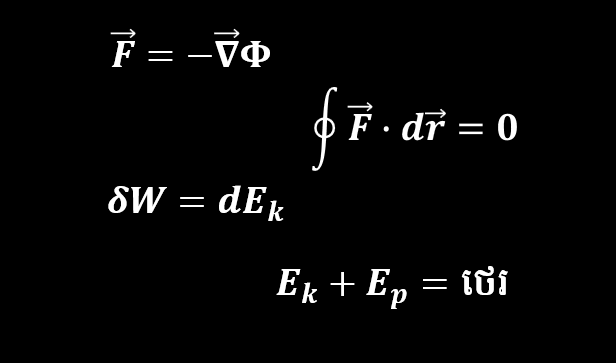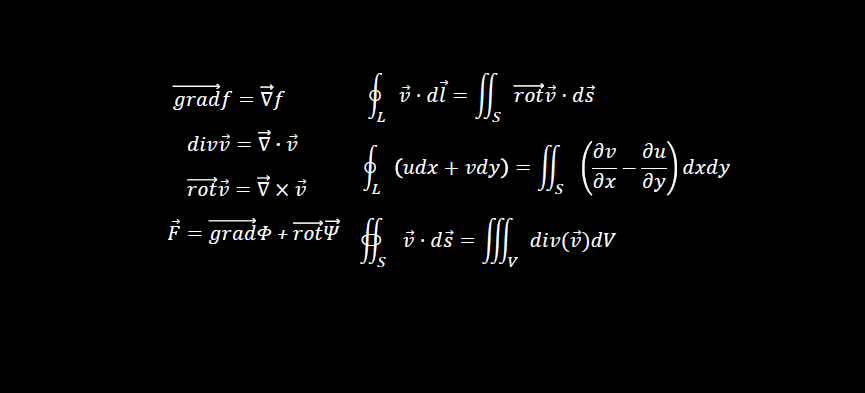កម្មន្ត​ និង​ថាមពល Work and Energy

*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ​​ ឬអក្សរដិត។ ឧទាហរណ៍ដូចជា

 

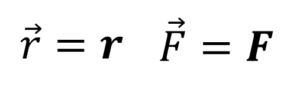
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ​ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។

អានុភាព Power

នៅក្នុងលំហសិក្សា R មានចំណុចរូបធាតុ A ធ្វើចលនាដោយល្បឿន v រងដែនកម្លាំំង F  ។ តាមនិយមន័យអានុភាព P នៃដែនកម្លាំង F បញ្ចេញលើ A កំណត់ដោយទំនាក់ទំនង

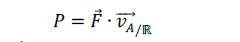
សិក្សាចលនាក្នុងតម្រុយដេកាតនោះកម្លាំង F កំណត់ដោយ

ហើយវ៉ិចទ័រទីតាំងនៃចំណុចរូបធាតុ A កំណត់ដោយ

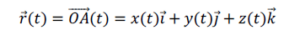
នោះគេបានល្បឿននៃ​ A គឺ

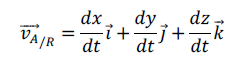
តាមផលគុណស្កាលែអានុភាពកំណត់ដោយ

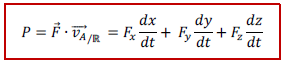
កម្មន្ត Work

កម្មន្តនៃដែនកម្លាំង F មានអំពើលើចំណុចរូបធាតុ A ត្រង់ចំណុច M_i(initial) ធ្វើឲ្យវាផ្លាស់ទីទៅចំណុច M_f (final) កំណត់ដោយទំនាក់ទំនង

ទម្រង់ឌីផេរ៉ង់ស្យែល

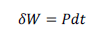
តាមការបកស្រាយអំពីអានុភាពដូចខាងលើគេបាន

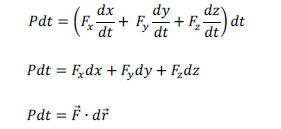
ដូចនេះទម្រង់ឌីផេរ៉ង់ស្យែលនៃកម្មន្តគឺ

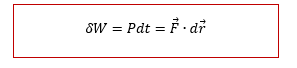
ហើយគេបានទម្រង់អាំងតេក្រាលនៃកម្មន្តគឺ

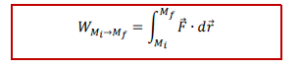
ឧទាហរណ៍ទី១ គណនាកម្មន្តនៃដែនកម្លាំង  មានអំពើ F = F(3x, -5z, 10x)​ មានអំពើរលើចំណុចរូបធាតុមួយធ្វើឲ្យវាផ្លាស់ទីតាមគន្លងដែលមានសមីការបារ៉ាមែត្រដូចខាងក្រោម

ចម្លើយ

ទម្រង់អាំងតេក្រាលនៃកម្មន្ត

វ៉ិចទ័រទីតាំងនៃចំណុចរូបធាតុ

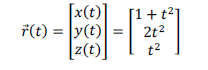
គេបានឌីផេរ៉ង់ស្យែលបន្លាស់ទីគឺ

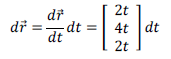
កម្លាំង F អាចធ្វើឲ្យអង្គធាតុផ្លាស់ទីតាមគន្លង (C) បានលុះត្រាតែខ្សែកោង (C) ស្ថិតនៅក្នុងលំហនៃដែនកម្លាំង F ពោលគឺខ្សែដែនកម្លាំង F ពិតជាកាត់តាមខ្សែកោង (C) មែន។

(C) ∈ F ⇔ សមីការខ្សែកោង (C)​ផ្ទៀងផ្ទាត់ក្នុងដែនកម្លាំង F

គេបាន

 

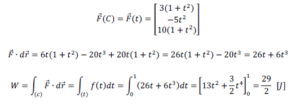
ថាមពលស៊ីនេទិច Kinetic Energy

ថាមពលស៊ីនេទិច E_k នៃចំណុចរូបធាតុ A មានម៉ាស m ក្នុងតម្រុយសិក្សា R ណាមួយកំណត់ដោយ

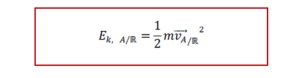
ក្នុងតម្រុយកាលីឡេ(ដេកាត) R គេមាន F គឺជាកម្លាំងដែលមានអំពើលើចំណុចរូបធាតុ A មានម៉ាស m ។

ច្បាប់គ្រឹះឌីណាម៉ិច

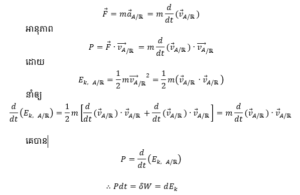
ទ្រឹស្តីបទថាមពលស៊ីនេទិច : ក្នុងតម្រុយកាលីឡេបម្រែបម្រួលថាមពលស៊ីនេទិចនៃរូបធាតុរវាងខណៈពីរគឺជាបម្រែបម្រួលកម្មន្តនៃកម្លាំងដែលបង្កើតឲ្យមានបម្លាស់ទី។

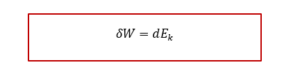
កម្លាំងរក្សា Conservative Force

គេថា F គឺជា(ដែន)កម្លាំងរក្សាលុះត្រាតែកម្លាំងនេះអាចទាញចេញពីអនុគមន៍ស្កាលែ (E_p) ណាមួយក្រោមទម្រង់

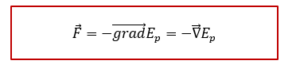
អនុគមន៍ស្កាលែ E_p ហៅថាប៉ូតង់ស្យែល ឬ សក្តានុពលនៃ F ។ ក្នុងការអនុវត្តជាក់ស្តែង E_p ហៅថាថាមពលប៉ូតង់ស្យែល(Potential Energy)នៃកម្លាំង F ។

លក្ខណៈនៃកម្លាំងរក្សា : ប្រសិនបើ F គឺជា(ដែន)កម្លាំងរក្សានោះគេបាន

(១) កម្មន្តនៃកម្លាំង F មិនអាស្រ័យនឹងរាងនៃបម្លាស់ទីនោះទេ ពោលគឺវាអាស្រ័យតែលើទីតាំងដើមនិងទីតាំងស្រេចតែប៉ុណ្ណោះ។ ហើយកម្មន្តនេះមានតម្លៃផ្ទុយនឹងបម្រែបម្រួលថាមពលប៉ូតង់ស្យែលរវាងពីរចំណុចនោះ។

ទម្រង់ឌីផេរ៉ងស្យែល

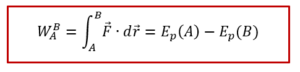
ទម្រង់អាំងតេក្រាល

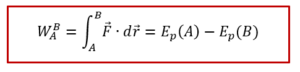
ក្នុងន័យដូចគ្នានេះដែរ ចំពោះករណីគន្លងនៃបម្លាស់ទីជាចលនាវិលវល់(ខ្សែបិទ) ឬទីតាំងដើមនឹងទីតាំងស្រេចត្រួតគ្នា នោះកម្មន្តនៃកម្លាំងរក្សាស្មើនឹងសូន្យ។

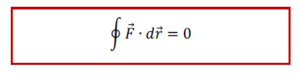
(២)​ ដែនកម្លាំងជាដែនមិនវិលឬនិយាយម្យ៉ាងទៀតថារង្វិលរបស់វាស្មើរសូន្យ។

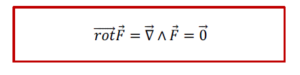
បំណកស្រាយ

ចំពោះអនុគមន៍ស្កាលែ E_p(x ,y ,z)ណាមួយក្នុងលំហគេបាន

 

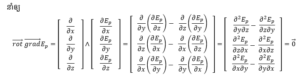
ប្រសិនបើមានដែនកម្លាំង F(x, y ,z) ណាមួយផ្ទៀងផ្ទាត់ទំនាក់ទំនង

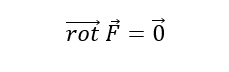
នោះគេទាញបាន

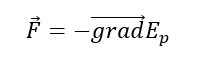
សញ្ញាដកបញ្ជាក់ថាថាមពលប៉ូតង់ស្យែលថយចុះព្រោះកម្លាំងត្រូវបានបញ្ចេញដើម្បីធ្វើឲ្យចំណុចរូបធាតុផ្លាស់ទីតាមគោលដៅ។

ឧទាហរណ៍ គេមានដែនកម្លាំង F កំណត់ក្នុងតម្រុយ R=OXYZ ចំពោះគ្រប់ចំណុច M(x,y,z) នៃលំហគេបាន F = F(F_x , F_y , F_z) ; F_x = k(yz-2xy), F_y = k(xz-x²), F_z = kxy ដែល k ជាចំនួនថេរ ។

១/ បង្ហាញថា F ជាក្រាដ្យង់នៃថាមពលប៉ូតង់ស្យែលណាមួយ។

២/ គណនាកម្មន្តនៃចំណុច M ដែលផ្លាស់ទីពី M₁(0,0,0)ទៅ M₂(1,1,0)តាមគន្លងនីមួយៗខាងក្រោម៖

ក-M₁ →A(1,0,0)→M₂

ខ– សមីការគន្លង

 គ– ផ្លាស់ទីដោយសេរី(គ្មានគន្លងកំណត់ច្បាស់លាស់)

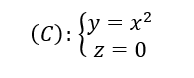
ចម្លើយ

១/

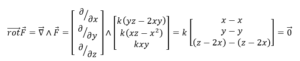
ចំពោះអនុគមន៍ស្កាលែ E_p(x,y,z)ណាមួយក្នុងលំហគេបាន

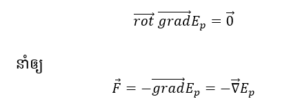
២/

ក-

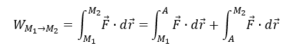
ក្នុងចន្លោះ M₁→A គេបានសមីការគន្លងគឺជាបន្ទាត់ (C) : y = 0 (z = 0)

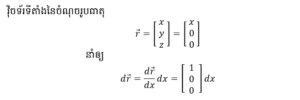
(C) ∈ F សមីការខ្សែកោង​​ (C) ផ្ទៀងផ្ទាត់ក្នុងដែនកម្លាំង​ F

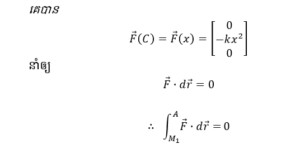
ក្នុងចន្លោះ A→M₂ គេបានសមីការគន្លងគឺជាបន្ទាត់​ (C) : x = 1 (z =0)

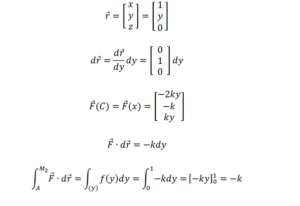
ដូចនេះ

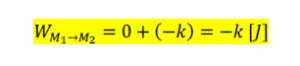
ខ-

សមីការគន្លង

គ-ករណីទូទៅមិនអាស្រ័យនឹងគន្លង

ការបកស្រាយក្នុងឧទាហរណ៍នេះបញ្ជាក់ពិលក្ខណៈនៃដែនកម្លាំងរក្សា។

អនុវត្តន៍កម្លាំងរក្សា

ថាមពលប៉ូតង់ស្យែលទំនាញដី Potential Energy

អង្គធាតុមានម៉ាស​ m​ ស្ថិតនៅកម្ពស់ h​₁ ពីផ្ទៃផែនដី(កម្ពស់ស្មើរសូន្យ)។ ប្រសិនបើគេលើកអង្គធាតុនេះដាក់នៅកម្ពស់ h₂ តើគេត្រូវប្រើប្រាស់ថាមពលអស់ប៉ុន្មាន?

ដោយមិនគិតកម្លាំងទប់នៃខ្យល់នោះកម្លាំងដែលមានអំពើលើអង្គធាតុមានតែមួយទេគឺកម្លាំងទំនាញដីឬទម្ងន់ P(gravitational force, weight)

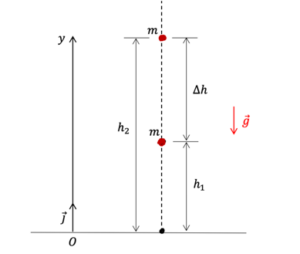
នាំឲ្យ P = mg គឺជាដែនកម្លាំងរក្សា

មានន័យថា P អាចទាញចេញពីថាមពលប៉ូតង់ស្យែល E_p ណាមួយតាមទំនាក់ទំនង

ដូចនេះដែនកម្លាំងទំនាញដីគឺជាដែនរក្សាហើយបម្រែបម្រួលថាមពលប៉ូតង់ស្យែលរវាងចំណុចពីរចំណុចកំណត់ដោយ

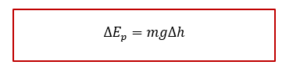
ថាមពលប៉ូតង់ស្យែលយឺតនៃរ៉ឺស័រ Potential Energy of a Spring

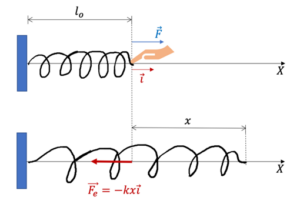
ប្រសិនបើយើងប្រើកម្លាំង F ទាញរ៉ឺស័រមួយបានប្រវែង​ x នោះរ៉ឺស័រនឹងបញ្ចេញកម្លាំងរារាំងទំនាញនេះដែលមានតម្លៃស្មើគ្នាតែមានទិសផ្ទុយពីកម្លាំងទាញនេះ។​ នេះហៅថាកម្លាំងយឺតនៃរ៉ឺស័រ​។​កម្លាំងយឺតនៃរ៉ឺស័រកំណត់ដោយ F_e=kx​ ដែល k ជាថេរកម្រាញនៃរ៉ឺស័រ​​​។​ ថេរកម្រាញកំណត់ពីភាពយឺតនៃរ៉ឺស័រផ្សេងៗ។

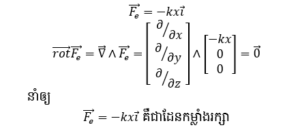
គេបាន F_e អាចទាញចេញពីថាមពលប៉ូតង់ស្យែល E_p ណាមួយតាមទំនាក់ទំនង

ជាទូទៅត្រង់ទីតាំងដើមឬទីតាំងលំនឹងរ៉ឺស័រគ្មានបន្លាស់ទី(គ្មានកម្លាំងរុញឬទាញ)ទេ ដូចនេះគេបាន E_p(0) = 0 ដូចនេះកម្លាំងយឺតនៃរ៉ឺស័រគឺជាកម្លាំងរក្សាហើយថាមពលប៉ូតង់ស្យែលយឺតរបស់វាកំណត់ដោយ

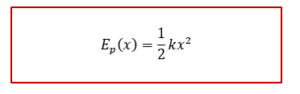
ថាមពលប៉ូតង់ស្យែលអេឡិចត្រូស្តាទិច Electric Potential Energy

ប៉ូតង់ស្យែលនៃដែនអគ្គីសនី Electric Potential

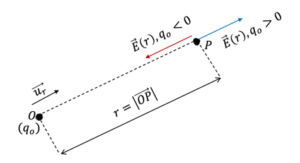
បន្ទុកអគ្គីសនី q_o ត្រង់ចំណុច O បង្កើតដែនអគ្គីសនី E ត្រង់ចំណុច P ដែលមានចម្ងាយពី r កំណត់ដោយ

នាំឲ្យ E គឺជាដែនរក្សា

មានន័យថា E អាចទាញចេញពីអនុគមន៍ប៉ូតង់ស្យែលស្កាលែ V ណាមួយតាមទំនាក់ទំនង

ដូចនេះដែនអគ្គីសនីអេឡិចត្រូស្តាតិចគឺជាដែនរក្សាហើយប៉ូតង់ស្យែលត្រង់ចំណុចមួយនៃដែននេះកំណត់ដោយ

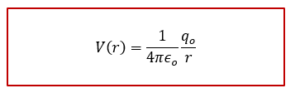
តាមសម្រាយខាងលើជាទូទៅប៉ូតង់ស្យែលនៃដែនអគ្គីសនីកំណត់ដោយ

 

ថាមពលប៉ូតង់ស្យែលអេឡិចត្រូស្តាទិច Electric Potential Energy

និយមន័យដែនអគ្គីសនីអេឡិចត្រូស្តាតិច :

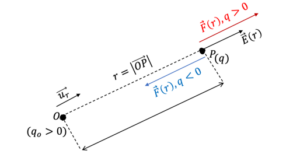
ដើម្បីងាយស្រួលក្នុងការសិក្សាយើងលើកករណី q₀ > 0 មកធ្វើជាឧទាហរណ៍ដូចបង្ហាញក្នុងរូបខាងលើ។ ប្រសិនបើត្រង់ចំណុច P គេដាក់បន្ទុកអគ្គីសនី q ណាមួយចូលក្នុងដែនអគ្គីសនី E នោះបន្ទុក q   នឹងរងកម្លាំងអគ្គីសនី F ដែលបង្កើតដោយដែនអគ្គីសនី E ក្រោមទម្រង់

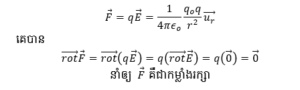
មានន័យថា F អាចទាញចេញពីថាមពលប៉ូតង់ស្យែល Ep ណាមួយ តាមទំនាក់ទំនង

ជាទូទៅថាមពលប៉ូតង់ស្យែលអគ្គីសនីស្តាទិចនៃបន្ទុកអគ្គីសនីកំណត់ដោយ

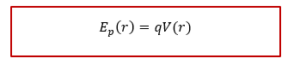
ថាមពលមេកានិច Mechanics Energy

ថាមពលមេកានិច  E_m នៃចំណុចរូបធាតុគឺជាផលបូកនៃថាមពលស៊ីនេទិចនិងថាមពលប៉ូតង់ស្យែល។

ពំនោលច្បាប់រក្សាថាមពល : ប្រសិនបើកម្លាំងដែលធ្វើឲ្យអង្គធាតុមានចលនាជាកម្លាំងរក្សា នោះថាមពលមេកានិចរបស់អង្គធាតុមិនបាត់បង់តាមទីតាំងបម្លាស់ទីនោះទេ គឺវាគ្រាន់តែប្តូរប្រភេទថាមពលតែប៉ុណ្ណោះ។

កម្លាំងមិនរក្សា (Nonconservative Force)

កម្លាំងណាមួយដែលផ្ទៀងផ្ទាត់លក្ខខ័ណ្ឌពីរខាងក្រោមហៅថាកម្លាំងមិនរក្សា ៖

(១) កម្មន្តនៃកម្លាំងដែលមានអំពើលើចំណុចរូបធាតុគឺជាកម្មន្តអវិជ្ជមាន

(២) កម្លាំងនេះមិនអាចទាញចេញពីថាមពលប៉ូតង់ស្យែលណាមួយទេ។

ថាមពលមេកានិចនៃកម្លាំងមិនរក្សា

នៅក្នុងបម្លាស់ទីនៃចំណុចរូបធាតុ ពេលខ្លះប្រភេទកម្លាំងប្រែប្រួលតាមចន្លោះសិក្សា(ទីតាំង)។ ក្នុងករណីនេះថាមពលសរុបនៃចំណុចរូបធាតុគឺជាថាមពលសរុបនៃកម្លាំងនីមួយៗពោលគឺកម្លាំងរក្សា និងកម្លាំងមិនរក្សា។

នេះមានន័យថាថាមពលមេកានិចដែលខាតបង់មានតម្លៃស្មើនឹងកម្មន្តនៃកម្លាំមិនរក្សា។