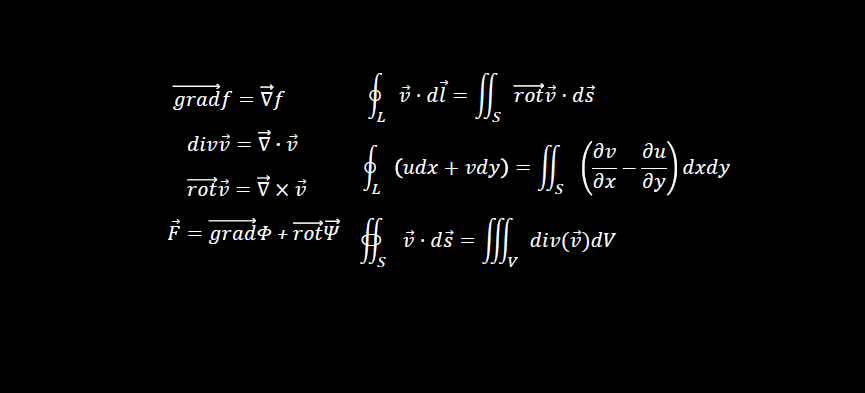*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ ឬអក្សរដិត។ ឧទាហរណ៍ដូចជា
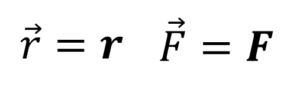
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។
===============================
វ៉ិចទ័របន្លាស់ទី និងចម្ងាយចរ Displacement Vector and Distance
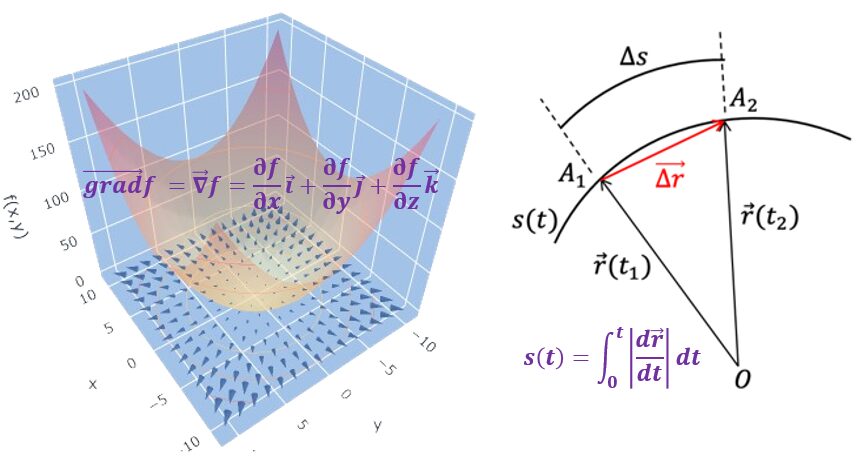
ក្នុងរយពេល t ចំណុចរូបធាតុ A((x(t), y(t), z(t)) ផ្លាស់ទីក្នុងលំហបង្កើតបានជាគន្លង (C) ។ ទីតាំងនៃចំណុចរូបធាតុ A អាស្រ័យនឹងប៉ារ៉ាមែត t កំណត់ដោយវ៉ិចទ័រទីតាំង
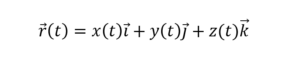
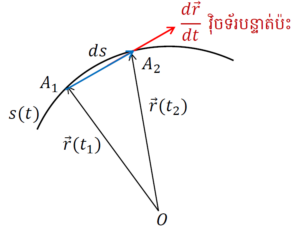
ដែលជាអនុគមន៍វ៉ិចទ័រ។ ដូចរូបខាងក្រោម យើងពិនិត្យមើលខ្សែកោង (C) នៅចន្លោះថេរវេលា t1 ≤ t ≤ t2។ ខណពេល t = t1 ចំណុចរូបធាតុនៅត្រង់ A1 ហើយ t = t2 ចំណុចរូបធាតុផ្លាស់ទីដល់ A2។ A1A2 = Δr = r(t1)-r(t2)នេះហៅថាវ៉ិចទ័របន្លាស់ទី(Displacement Vector) ។
ប្រវែងខ្សែកោង s គឺជាផលបូកចូលគ្នានៃអង្កត់តូចៗ Δs លើខ្សែកោង ហើយយើងអាចគណនាវាបានដោយសន្មតថាអង្កត់នីមួយៗមានទំហំតូចបំផុតឬលីមីតΔs→ 0។ តាំងតម្លៃលីមីតនេះដោយ ds នោះប្រវែងខ្សែ s កំណត់ដោយ
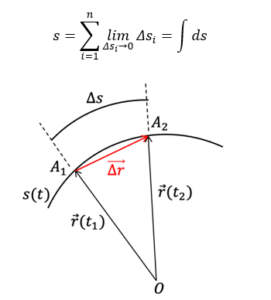
តែប្រវែង ds នៅចន្លោះ A1, A2ក៏ជាណមនៃវ៉ិចទ័រ dr ដែលជាឌីផេរ៉ង់ស្យែលនៃវ៉ិចទ័រទីតាំងដែរ។
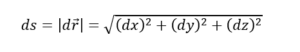
ដោយប្រវែងខ្សែប្រែប្រួលតាមពេលវេលា s =s(t) យើងអាចសរសេរ
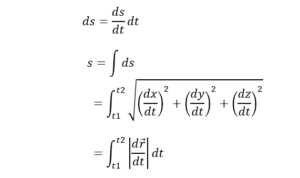
រូបមន្តនេះជារូបមន្តប្រវែងធ្នូ(Arc length)ហើយក្នុងមេកានិចនៃរូបធាតុគេហៅថា ចម្ងាយចរ(distance)នៃចំណុចរូបធាតុ។ ប្រសិនបើយើងគិតខណពេលដើម t1 = 0 ហើយខណពេលស្រេច t2 = t ណាមួយ។ នោះចម្ងាយចរនៃចំណុចរូបធាតុក្នុងចន្លោះពេលនោះគឺ
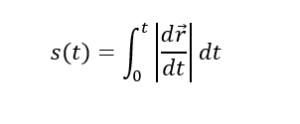
ដេរីវេអង្គសងខាងដោយ t
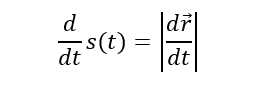
ដោយបង្ហាញក្នុងរូបខាងក្រោម ដោយហេតុថាដេរីវេនៃវ៉ិចទ័រទីតាំងធៀបនឹងពេល dr/dt ប៉ះនឹងខ្សែកោង (C) គ្រប់ចំណុចទើបគេហៅវ៉ិចទ័រនេះថា វ៉ិចទ័របន្ទាត់ប៉ះ(Tangent Vector)។ ដោយឡែកដូច r = r(s) ដែរយើងក៏អាចសរសេរវ៉ិចទ័រទីតាំងជាអនុគមន៍នៃប៉ារ៉ាមែត s ដែរ ពោលគឺ
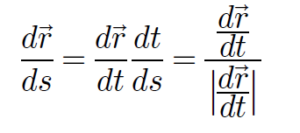
នេះគឺជាវ៉ិចទ័របន្ទាត់ប៉ះឯកតា(Unit Tangent Vector)។ តាងវ៉ិចទ័រនេះដោយ t នោះកំប៉ូសង់របស់វាគឺ
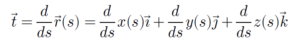
ឧទាហរណ៍ ចលនានៃចំណុចរូបធាតុមួយកំណត់ដោយវ៉ិចទ័រទីតាំង r(t) = asinti + acostj + btk។ គណនាចម្ងាយចរនៃចំណុចរូបធាតុលើខ្សែកោង C ក្នុងចន្លោះ t = 0 ទៅ ខណ t ណាមួយ។
ដំណោះស្រាយ
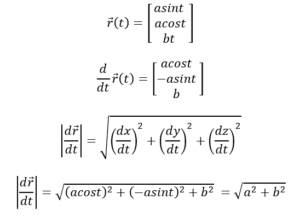
ចម្ងាយចរនៅខណពេល t គឺ
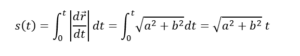
ចំណោតនៃដែនស្កាលែ Gradient of a Scalar Field
និយមន័យនិងការគណនា
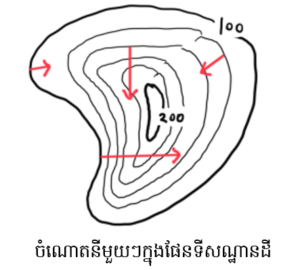
លំហដែលមានបរិមាណស្កាលែប្រែប្រួលតាមទីតាំងហៅថាដែនស្កាលែ (Scalar Field)។ ឧទាហរណ៍ដូចជាក្នុងផែនទីសណ្ឋានដី (Topographic Map) ក្នុងរូបភាពខាងក្រោមគឺជាដែនស្កាលែមួយ។ វាជាលំហដែលមានកម្ពស់ដី(ទំហំស្កាលែ)ប្រែប្រួលតាមទីតាំងផ្សេងៗ។ ក្នុងផែនទីសណ្ឋានដីបែបនេះ ចំណុចពីរស្ថិតនៅក្បែរគ្នាដែលមានកម្ពស់ខុសគ្នានាំឲ្យមានចំណោត(gradient)កើតឡើង។ ដូចគ្នាដែរចំពោះដែនស្កាលែនៃសីតុណ្ហភាពបរិយាកាសក៏មានចំណោតដែរនៅពេលដែលទីតាំងពីរក្បែគ្នាមានសីតុណ្ហភាពខុសគ្នា។ ចំណោតដូចបានរៀបរាប់មកនេះគឺជាទំហំដែលមានទាំងបរិមាណនិងទិសដៅពោលគឺវាជាទំហំវ៉ិចទ័រ។ ដូចនេះចំណោតនៃដែនស្កាលែគឺជាដែនវ៉ិចទ័រ (Vector Field)។
យក f(x, y, z) ជាដែនស្កាលែដែលមានបរិមាណស្កាលែ f ត្រង់ទីតាំង(x, y, z)។ អត្រាបម្រែបម្រួលនៃទំហំស្កាលែក្នុងដែនឬលំហស្កាលែ f(x, y, z) ហៅថាក្រាដ្យង់ឬចំណោត។ ក្នុងអត្ថបទនេះយើងប្រើតែពាក្យចំណោតទេ។ ចំណោតនេះគឺជាទម្រង់ដេរីវេដែលបង្ហាញអំពីបម្រែបម្រួលបរិមាណស្កាលែដ៏តូចធៀបនឹងបម្រែប្រួលទីតាំងដ៏តូច។ ដេរីវេដោយផ្នែកលើអញ្ញតិនីមួយៗនៃអនុគមន៍ស្កាលែក្លាយជាអត្រាបម្រែបម្រួលតាមទិសនីមួយៗ។ យើងអាចសរសររូបមន្តចំណោតដូចខាងក្រោម
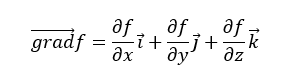
សញ្ញាណ grad ចេញមកពីពាក្យ gradient ដែលប្រែថា ចំណោត ភាពទេរ ភាពជ្រេជាដើម។ ដូចសមីការខាងលើ លក្ខណពិសេសនៃទីតាំងនីមួយៗក្នុងដែនត្រូវបានកំណត់ដោយការគណនាដេរីវេ។ សញ្ញាណ grad នៃចំណោតអាចសរសេរដោយប្រើប្រាស់សញ្ញាណដេរីវេណាប្លា(nabla)∇ ដូចខាងក្រោម
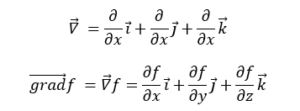
ដោយ gradf គឺជាវ៉ិចទ័រដែលទាញចេញពីដែនស្កាលែវាក៏ត្រូវបានគេហៅថាវ៉ិចទ័រចំណោត(gradient vector) ផងដែរ។ វ៉ិចទ័រចំណោតគឺជាវ៉ិចទ័រដែលត្រូវបានគណនាចេញពីអនុគមន៍ច្រើនអញ្ញាតិ។ ដូចជាឈ្មោះរបស់វាដែរ វ៉ិចទ័រចំណោតបង្ហាញអំពីទិសនិងទំហំនៃចំណោត(បម្រែបម្រួល)នៃអនុគមន៍ច្រើនអថេរ។
លក្ខណនៃទិសនិងទំហំនៃវ៉ិចទ័រចំណោតគឺ
ទិស : គឺជាទិសដែលអត្រាបម្រែបម្រួលនៃអនុគមន៍ច្រើនអថេរមានទំហំធំបំផុត
ទំហំ : គឺជាលំងាក(អត្រាបម្រែបម្រួល)នៃករណីទិសដូចខាងលើ
ឧទាហរណ៍ យើងនឹងពិនិត្យមើលវ៉ិចទ័រចំណោតនៃដែនស្កាលែ f(x, y) = x2 + y2 ។
ដែនស្កាលែ f(x, y, z) = x2 + y2 អាចគូជាផ្ទៃកោង (surface) ដូចរូបខាងក្រោម
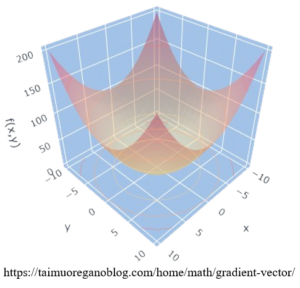
តាមរយរូបភាពនេះយើងឃើញថា ដែនស្កាលែ f មានតម្លៃតូចបំផុតនៅគល់តម្រុយហើយរីកធំទៅៗពេលដែលឃ្លាតឆ្ងាយពីគល់តម្រុយ។ ម្យ៉ាងទៀត បើយើងពិនិត្យមើលកូរអរដោយណេជិតគល់តម្រុយ និងចុងនៃអ័ក្សយើងនឹងឃើញថាទីតាំងផ្សេងៗត្រង់ចុងអ័ក្សមានមុំទេរធំជាងពោលគឺអត្រាបម្រែបម្រួលរបស់វាធំជាងត្រង់គល់តម្រុយ។
តាមនិយមន័យចំណោតនៃ f គឺ
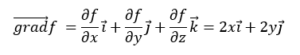
ចំពោះគ្រប់ចំណុច (x, y) គេបានរូបភាពនៃវ៉ិចទ័រចំណោតនៃដែនស្កាលែ f ដូចខាងក្រោម
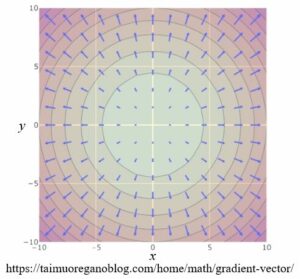
ដូចបង្ហាញក្នុងរូប ក្នុងករណីដែនស្កាលែមួយនេះ វ៉ិចទ័រចំណោត(ព្រួញពណ៌ខៀវ)គឺជាសំណុំវ៉ិចទ័រក្នុងប្លង់ដេក(xy)។ សញ្ញាព្រួញមានទិសសំដៅទៅទិសដែលដែនស្កាលែរីកធំឡើង។ ម្យ៉ាងទៀត ទំហំព្រួញធំទៅៗកាលណាវាឃ្លាតចេញពីគល់តម្រុយ។ នេះមានន័យថាទំហំអត្រាបម្រែបម្រួលនៃដែនស្កាលែកើនឡើងធំទៅៗត្រង់ទីតាំងឆ្ងាយពីគល់តម្រុយ។ បើយើងបញ្ចូលរូបភាពដែនជាមួយរូបភាពវ៉ិចទ័រចំណោតនោះគេបានរូបភាពដូចខាងក្រោម
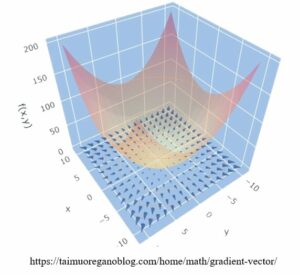
ទំនាក់ទំនងគ្រឹះនានានៃចំណោត
ចំពោះដែនស្កាលែ f និង g គេបានទំនាក់ទំនងគ្រឹះនៃចំណោតដូចខាងក្រោម។ α，β គឺជាចំនួនថេរ
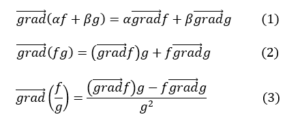
បំណកស្រាយ
ទំនាក់ទំនងទី(1)
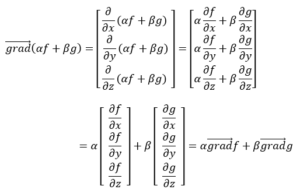
ទំនាក់ទំនងទី(2)
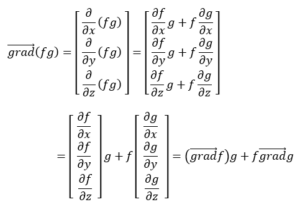
ទំនាក់ទំនងទី(3)
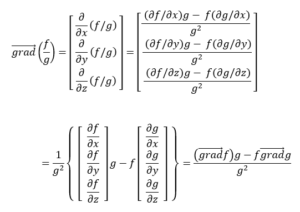
លំហាត់អនុវត្តន៍
(1) ចលនារបស់អង្គធាតុមួយកំណត់ដោយវ៉ិទ័រទីតាំង
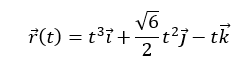
គណនាចំងាយចរត្រង់ខណពេល t ណាមួយនៃចលនា។
(2) គណនាវ៉ិចទ័រចំណោតនៃដែនស្កាលែ
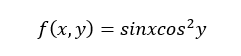
(3) ចំពោះវ៉ិចទ័រទីតាំង
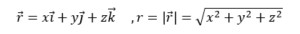
ចូរគណនា gradln(r) ជាអនុគន៍នៃ r និង r។
ចម្លើយគម្រូ
(1)
(2)
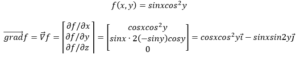
(3)
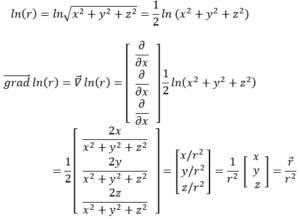
ឯកសារយោង
薩摩順吉：物理の数学，岩波書店，1995,pp.91-95, 101-107
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
