*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា
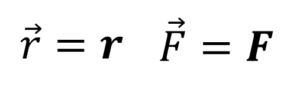
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។
==============================
បន្សាយនៃដែនវ៉ិចទ័រ Divergence of a Vector Field
ដោយសារតែសញ្ញាណដេរីវែណាប្លា (nabla) គឺជាទំហំវ៉ិចទ័រ (∇ = ∂/∂xi+∂/∂yj+∂/∂zk ) គេត្រូវគិតពីលទ្ធភាពពីរផ្សេងគ្នាពេលវ៉ិចទ័រណាប្លា∇ ធ្វើផលគុណ(ស្កាលែឬខ្វែង)ជាមួយនឹងវ៉ិចទ័រ A ណាមួយ។ ផលគុណស្កាលែរវាងណាប្លានឹងវ៉ិចទ័រ (∇・A ) ទទួលបានបន្សាយ(Divergence) ហើយផលគុណខ្វែងរវាងណាប្លានឹងវ៉ិចទ័រ(∇×A ) ទទួលបានរង្វិល(Curl, Rotation)។ ដំបូងយើងនឹងសិក្សាលើបន្សាយមុន។ ដើម្បីសម្រួលដល់ការសិក្សាយើងនឹងពិនិត្យដែនលឿនលំហូរនៃសន្ទនីយ៍ក្នុងប្លង់ពីរវិមាត្រ។
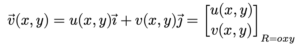
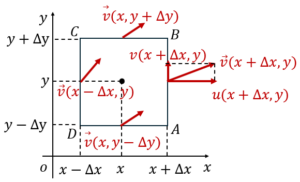
យើងនឹងពិនិត្យចលនាចេញចូលនៃសន្ទនីយ៍ក្នុងផ្ទៃ ABCD (ផ្ចិត(x, y))ក្នុងប្លង់ដេក(xy)ដែលប្រវែងតាមអ័ក្សដេកគឹ 2Δx ហើយប្រវែងតាមអ័ក្សឈរគឺ 2Δy។ វ៉ិចទ័រល្បឿនលំហូរប្រែប្រួលតាមទីតាំងនីមួយៗ។ ត្រង់ចំណុចកណ្តាលអង្កត់ AB គឺv(x+Δx, y) ត្រង់ចំណុចកណ្តាល BC គឺv(x, y+Δy) ត្រង់ចំណុចកណ្តាល CD គឺv(x-Δx, y) ត្រង់ចំណុចកណ្តាល DA គឺv(x, y-Δy)។ ដោយសារវាជាសន្ទនីយ៍ពីរវិមាត្រ ដូចនេះដែនល្បឿនលំហូរគ្មានកំប៉ូសង់តាមទិសដែលកែងនឹងប្លង់ (xy) (ទិស z)នោះទេ។ យើងអាចសរសរកំប៉ូសង់ត្រង់ទីតាំងនីមួយៗតាម វ៉ិចទ័រដូចខាងដូចខាងក្រោម
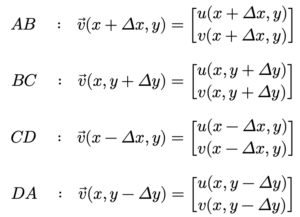
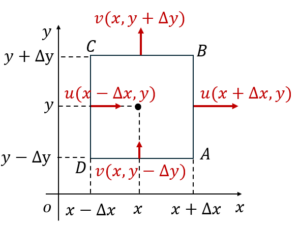
សន្មតថាទិសនៃសន្ទនីយ៍ហូរចេញពី ABCD ជាទិសវិជ្ជមាន។ ចំពោះអង្កត់ AB បរិមាណសន្ទនីយ៍ QAB អាចគណនាបានដោយផលគុណរវាងល្បឿនលំហូរ u(x+Δx, y)នឹងប្រវែងអង្កត់2Δy ។ ផ្នែកផ្សេងៗទៀតក៏ដូចគ្នាដែរគឺ
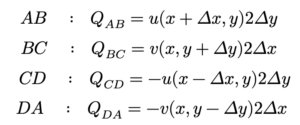
ដោយទិសសន្ទនីយ៍ហូរចេញជាទិសវិជ្ជមាន នោះទិសដែលផ្ទុយនឹងទិសនៃអ័ក្ស x និងអ័ក្ស y ត្រូវមានសញ្ជាដក។ ដូចនេះបរិមាណលំហូរសរុប Q ចេញពី ABCD គឺ
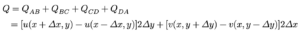
ចំពោះ u និង v គេអាចប្រើពន្លាតតៃល័រ (Taylor Series or Expansion)ធៀបនឹងអញ្ញតិ (x,y) ដូចខាងក្រោម
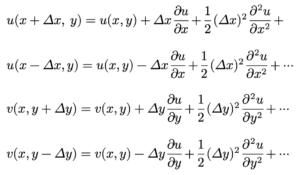
ដោយមិនគិតតម្លៃចាប់ពីរដេរីវេទី៣ទៅ បរិមាណលំហូរសរុប Q គឺ
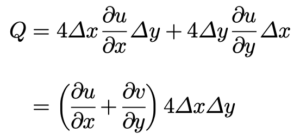
ដោយ 4ΔxΔy គឺជាក្រលាផ្ទៃ ABCD ដូចនេះបរិមាណលំហូរក្នុងមួយខ្នាតផ្ទៃ D គឺ
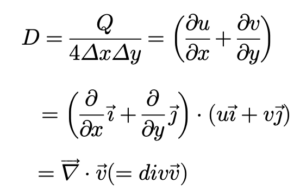
នេះគឺជាបន្សាយឬឌីវែសង់នៃដែនវ៉ិចទ័រ v។ ដោយក្នុងភាសាអង់គ្លេសគេប្រើពាក្យ divergence និមិត្តសញ្ញបន្សាយគឺ div ។ ក្នុងវែបសាយនេះយើងប្រើតែពាក្យបន្សាយតែប៉ុណ្ណោះ។
ចំពោះដែនវ៉ិចទ័របីវិមាត្រ
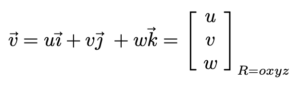
គេបានបន្សាយនៃ v គឺ
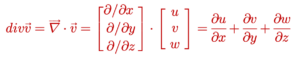
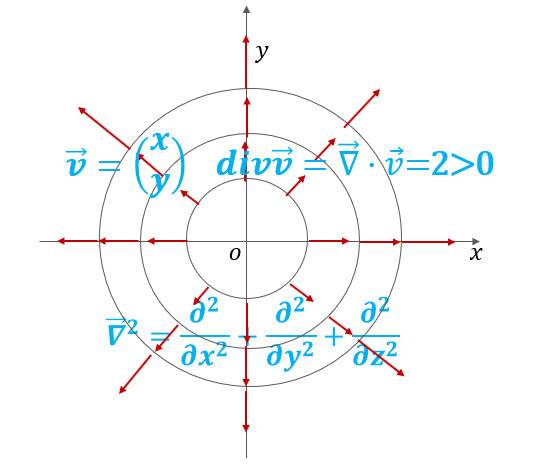
ដូចបានរៀបរាប់ខាងលើ divv គឺជាបរិមាណចេញចូលក្នុងមួយខ្នាតផ្ទៃ(ឬមាឌ)នៃដែនវ៉ិចទ័រ។ ចំពោះឧទាហរណ៍ខាងលើ ករណី divv > 0 លំហូរចេញពីផ្ទៃមានបរិមាណច្រើនជាងលំហូចូលផ្ទៃ ហើយសន្ទនីយ៍ចាប់ផុសចេញក្រៅត្រង់ទីតាំងនោះ។ លំហូបែបនេះហៅថា លំហូររីក(លំហូដែលមានបន្សាយចេញ)។ ផ្ទុយទៅវិញករណី divv < 0 លំហូរចូលក្នុងផ្ទៃមានទំហំធំជាងលំហូចេញ គេថាសន្ទនីយ៍ស្រូបទាញចូលត្រង់ទីតាំងនោះ។ លំហូរបែបនេះហៅថា លំហូររួម(លំហូដែលមានបន្សាយចូល)។
នៅក្នុងវារីសាស្ត្រ(Hydraulics)ចំពោះសន្ទនីយ៍បីវិមាត្រ ប្រសិនបើគ្មានហេតុណាមួយសមស្របទេសន្ទនីយ៍មិនផុសចេញក្រៅហើយក៏មិនស្រូបចូលក្នុងដែរ។ ហេតុនេះបន្សាយនៃដែនវ៉ិចទ័រត្រូវស្មើសូន្យ។
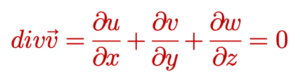
សមីការនេះហៅថា សមីការនិរន្តរភាពដែលអនុវត្តចំពោះសន្ទនីយ៍មិនរងសម្ពាធ(incompressible fluid)។
ឧទាហរណ៍ គណនាបន្សាយនៃដែនវ៉ិចទ័រខាងក្រោម
(1) v =xi+yj
(2) v=yi-xj
ចម្លើយគម្រូ
(1)
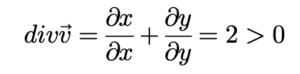
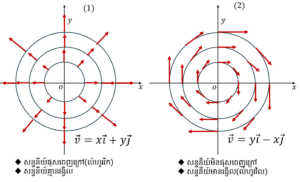
ដូចនេះដែនវ៉ិចទ័រនេះជាលំហូររីក។ ដូចបង្ហាញក្នុងរូបខាងក្រោមដែនវ៉ិចទ័រ v =xi+yj គឺជាលំហូដែលផុសចេញខាងក្រៅប្រៀបដូចជាការបញ្ចេញរស្មីមានគល់តម្រុយជាផ្ចិត។
(2)
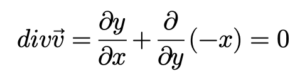
ដូចនេះដែនវ៉ិចទ័រនេះជាដែនវ៉ិចទ័រមិនរីកមិនរួម។ ដូចបង្ហាញក្នុងរូបខាងក្រោមដែនវ៉ិចទ័រ v =yi – xj គឺជាលំហូរដែលវិលជុំវិញគល់តម្រុយមិនផុសចេញក្រៅឬស្រូបចូលក្នុងទេ។
ទំនាក់ទំនងគ្រឹះនៃបន្សាយ
ចំពោះដែនវ៉ិទ័រ A, B ដែនស្កលែφ ចំនួនពិត α，β គេបានទំនាក់ទំនងខាងក្រោម
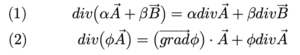
បំណកស្រាយ ៖ យក A = (Ax, Ay, Az), B = (Bx, By, Bz)
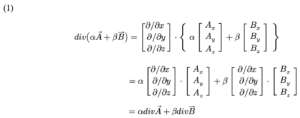
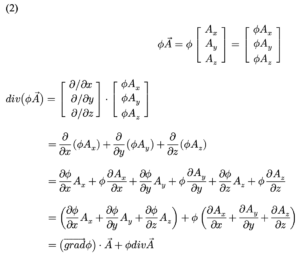
សញ្ញាណឡាផ្លាស Laplacian
ចំពោះដែនស្កាលែ φចំណោតកំណត់ដោយ gradφ=∇φ ដែលជាអនុគមន៍វ៉ិចទ័រ។ សាកល្បងគណនាបន្សាយនៃចំណោត
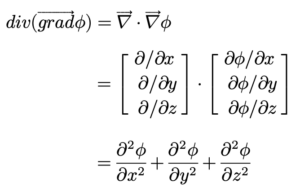
តាងផលគុណស្កាលែនៃណាប្លាជាមួយនឹងខ្លួនឯងដោយ ∇・∇=∇2 ឬ Δ ។ សញ្ញាណដេរីវេមួយនេះហៅថាឡាប្លាស(Laplacian)។
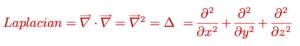
សមីការ Laplacian(φ) = 0 ហៅថាសមីការឡាផ្លាស ហើយអនុគមន៍φ ដែលផ្ទៀងផ្ទាត់ទំនាក់ទំនងនេះហៅថា អនុគមន៍អាកម៉ូនិច(Harmonic Function)។
ឧទាហរណ៍ កំណត់សមីការឡាផ្លាសនៃដែនស្កាលែφ=x3+sin(yz)។
ចម្លើយគម្រូ
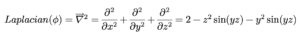
សមីការឡាផ្លាសគឺ
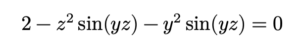
លំហាត់អនុវត្ត
1/ គណនាបន្សាយនៃដែនវ៉ិចទ័រខាងក្រោម
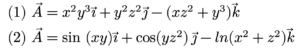
2/ ចំពោះវ៉ិចទ័រទីតាំង
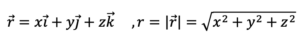
ចូរគណនាបន្សាយខាងក្រោម
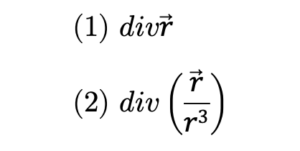
ចម្លើយគម្រូ
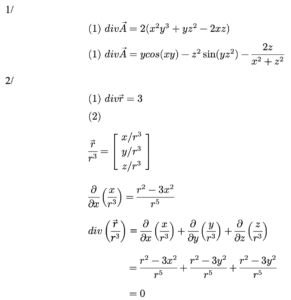
ឯកសារយោង
薩摩順吉：物理の数学，岩波書店，1995, pp.96-99
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
