អនុគមន៍វ៉ិចទ័រអថេរទោល Vector Functions of a Singular Variable

*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ​​ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា

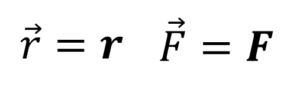
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ​ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។

===========================

ទីតាំងនៃចំណុចរូបធាតុក្នុងលំហ​(តម្រុយសិក្សា)

ចលនារបស់ចំណុចរូបធាតុតែងតែប្រព្រឹត្តទៅនៅក្នុងលំហត្រីវិមាត្រ R ណាមួយហើយរបស់វាតែងប្រែប្រួលតាមពេលវេលា t (time)។ ហេតុនេះហើយជាទូទៅចលនានៃចំណុចរូបធាតុត្រូវបានកំណត់ដោយអនុគមន៍បួនអថេរ(លំហបីវិមាត្រ+ពេល) f(space, time) = f(x,y,z,t)។ ជាទូទៅទីតាំងនៃចំណុចរូបធាតុត្រូវបានកំណត់ដោយវ៉ិចទ័រទីតាំង r(t) ណាមួយ។ វ៉ិចទ័រទីតាំងនេះជាអនុគន៍វ៉ិចទ័រអថេរទោលពោលគឺពេលវេលា t ជាអថេរហើយទីតាំង r ជាអនុគមន៍។ របៀបនៃការសរសេរវ៉ិចទ័រទីតាំងប្រែប្រួលអាស្រ័យទៅលើតម្រុយសិក្សា។

តម្រុយដេកាត(Cartesian Coordinate)

ក្នុងតម្រុយដេកាត R = oxyz វ៉ិចទ័រទីតាំង r(t) នៃចំណុចរូបធាតុ A(x, y, z) កំណត់ដោយ

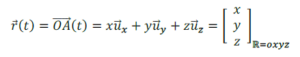
ដែល u_x, u_y, u_z ជាវ៉ិចទ័រឯកតារៀងគ្នាលើអ័ក្ស(ox), (oy), (oz)

តម្រុយប៉ូលែ(Polar Coordinate)

ក្នុងតម្រុយប៉ូលែ R = oρφ វ៉ិចទ័រទីតាំង r(t) នៃចំណុចរូបធាតុ A(ρ, φ) កំណត់ដោយ

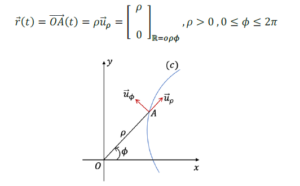
ដែល​ u_ρ ជាវ៉ិចទ័រឯកតាតាមទិសកាំ OA , u_φ វ៉ិចទ័រឯកតាតាមទិសកំណោងដេលកែងនឹង OA  , ρ ហៅថាកាំប៉ូលែ, ​ φ​ ហៅថាមុំប៉ូលែ

ទំនាក់ទំនងរវាងប្លង់ដេកាត(oxy) និងប្លង់ប៉ូលែ

 

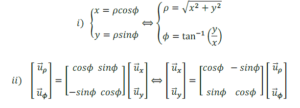
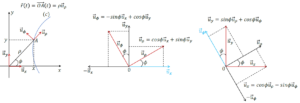
តម្រុយស៊ីឡាំង(Cylindrical Coordinate)

ប្រសិនបង្កើនកម្រាស់ប្លង់ប៉ូលែដោយតម្លៃ z នោះគេបានតម្រុយស៊ីឡាំង R = oρφz ហើយវ៉ិចទ័រទីតាំង r(t) នៃចំណុចរូបធាតុកំណត់ដោយ

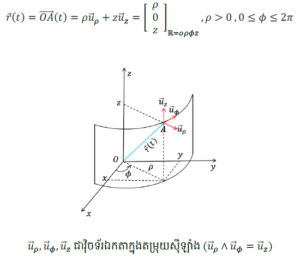
គេបានទំនាក់ទំនងរវាងតម្រុយស៊ីឡាំងនិងតម្រុយដេកាតគឺ

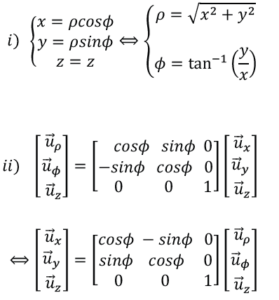
តម្រុយស្វ៊ែ(Spherical Coordinate)

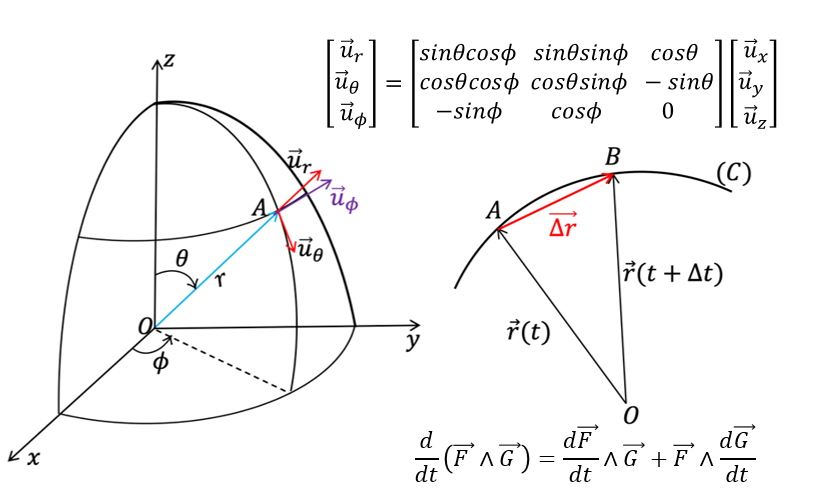
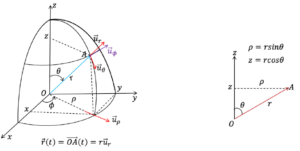
ប្រសិនបើគេបង្វិលប្លង់ប៉ូលែដោយមុំ 0～180ដឺក្រ គេបានតម្រុយស្វ៊ែ R = orθφ​ហើយវ៉ិចទ័រទីតាំង r(t) នៃចំណុចរូបធាតុកំណត់ដោយ

ទំនាក់ទំនងរវាងតម្រុយស្វ៊ែ តម្រុយស៊ីឡាំង និងតម្រុយដេកាត

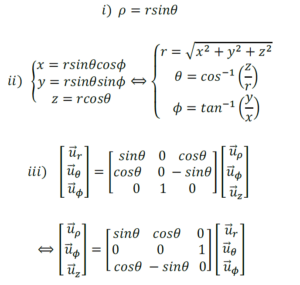
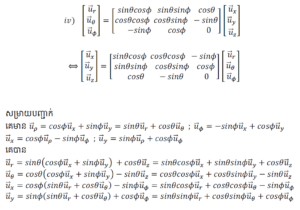
អនុគមន៍វ៉ិចទ័រអថេរទោល Vector Functions of a Singular Variable

ឌីផេរ៉ង់ស្យែល (Differentiation)

ទ្រឹស្តីអនុគមន៍វ៉ិចទ័រមានលក្ខណៈដូចគ្នានឹងអនុគមន៍ចំនួនពិតដែរ។ អនុគមន៍វ៉ិចទ័រ r(t) គឺជាទំនាក់ទំនងដែលភ្ជាប់វ៉ិចទ័រ r ជាមួយនឹងចំនួនពិត t ក្នុងចន្លោះសិក្សា(ដែនកំណត់)។ លក្ខណៈនៃលីមីតអាចយកមកអនុវត្តចំពោះអនុគមន៍វ៉ិចទ័របាន។

កន្សោម​ lim_t→tor(t) = R បញ្ជាក់ថាចំពោះគ្រប់ចំនួនវិជ្ជមានតូចបំផុត ε មានចំនួនពិតវិជ្ជមាន δ មួយដែល​ |r(t)-R|<ε ចំពោះ​ 0 < |t-t_o|< δ ។ គេបានណមនៃវ៉ិចទ័រ r ខិតជិតណមនៃវ៉ិចទ័រ R ហើយកំប៉ូសង់នៃ r ក៏ខិតជិតកំប៉ូសង់នៃ​ R ដែរ។

អនុគមន៍វ៉ិចទ័រ r ជាអនុគមន៍ជាប់ត្រង់ t_o លុះត្រាតែ

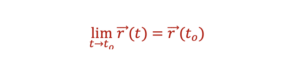
r(t)មានដេរីវេត្រង់ t_o លុះត្រាតែ

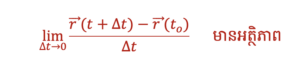
តម្លៃលីមីតនេះគឺជាដេរីវេនៃ r ត្រង់ t_o ។ អនុគមន៍ដេរីវេនៃអនុគមន៍វ៉ិចទ័រក៏ជាអនុគមន៍វ៉ិចទ័រដែរ។​

ជាទូទៅដេរីធៀបពេលនៃអនុគមន៍វ៉ីចទ័រ​ r(t) កំណត់ដោយ

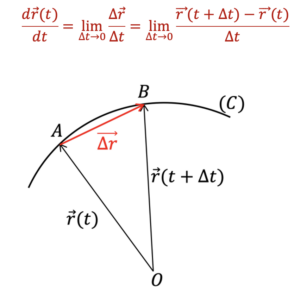
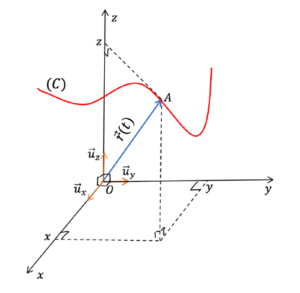
ដូចបង្ហាញក្នុងរូបខាងលើ (C) គឺជាគន្លងនៃចំណុចរូបធាតុណាមួយក្នុងលំហសិក្សា។

• នៅខណៈពេល t រូបធាតុស្ថិតត្រង់ចំណុច A ហើយមានវ៉ិចទ័រទីតាំង r(t)
• នៅខណៈពេល t + Δt រូបធាតុស្ថិតត្រង់ចំណុច B ហើយមានវ៉ិចទ័រទីតាំង r(t + Δt )

កាលណាចន្លោះពេលនៃបម្លាស់ទីខិតជិតសូន្យ (Δt → 0)នោះចំណុច B ស្ទើតែជាប់នឹងចំណុច A ហើយកន្សោម​ dr(t)/dt ក្លាយជាមេគុណប្រាប់ទិសនៃបន្ទាត់ប៉ះខ្សែកោង (C) ត្រង់ A  

ដេរីវេនៃវ៉ិចទ័រឯកតា

ជាទូទៅដេរីវេនៃអនុគមន៍វ៉ិចទ័រថេរណាមួយគឺជាវ៉ិចទ័រសូន្យ ហើយដេរីវេនៃវ៉ិចទ័រឯកតានៃតម្រុយនឹង(តម្រុយដេកាត)គឺជាវ៉ិចទ័រសូន្យ។

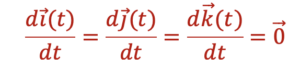
កំប៉ូសង់នៃអនុគមន៍ដេរីវេ

ឧទាហរណ៍ទី១ គណនាដេរីវេបន្តបន្ទាប់នៃអនុគមន៍វ៉ិចទ័រ A(t) = t³i + t²j+ (2-t)k

ដំណោះស្រាយ

ទ្រឹស្តីបទគ្រឹះនានា

ទ្រឹស្តីបទទី១ ៖ បើ F និង G ជាពីរអនុគមន៍វ៉ិចទ័រមានដេរីវេនោះ F + G ក៏ជាអនុគមន៍មានដេរីវេដែរ។ ដេរីវេនៃអនុគមន៍ F+G គឺជាផលបូកនៃដេរីវេនៃអនុគមន៍ F និង G ចូលគ្នា។

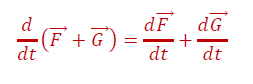
ទ្រឹស្តីបទទី២ ៖ បើ F ជាអនុគមន៍វ៉ិចទ័រមានដេរីវេ ហើយ S ជាអនុគមន៍ស្កាលែមានដេរីវេ នោះអនុគមន៍ SF​ គឺជាអនុគមន៍វ៉ិចទ័រមានដេរីវេ​ ហើយគេបានទំនាក់ទំនង

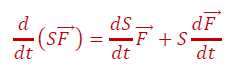
ទ្រឹស្តីបទទី៣ ៖ បើ F និង G ជាពីរអនុគមន៍វ៉ិចទ័រមានដេរីវេនោះ F・G ជាអនុគមន៍ស្កាលែមានដេរីវេហើយគេបាន

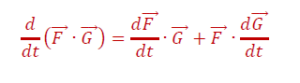
ទ្រឹស្តីបទទី៤ ៖ បើ F និង G ជាពីរអនុគមន៍វ៉ិចទ័រមានដេរីវេ នោះ F∧G ជាអនុគមន៍វ៉ិចទ័រមានដេរីវេ ហើយគេបាន

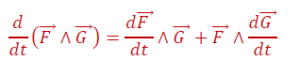
បំណកស្រាយ

 

ឧទាហរណ៍ទី២ ចំពោះវ៉ិចទ័រ​ a(t) ដែលមានណមថេរពោលគឺ​ |a(t) |= C ថេរ បង្ហាញថា a(t)​ និង da(t)/dt ជាពីរវ៉ិចទ័រកែងគ្នា។​

ដំណោះស្រាយ

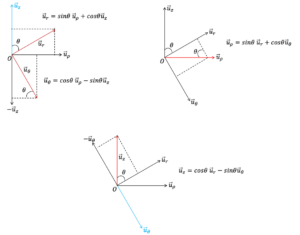
ដេរីវេវ៉ិចទ័រឯកតាក្នុងតម្រុយផ្សេងទៀត

តម្រុយប៉ូលែ

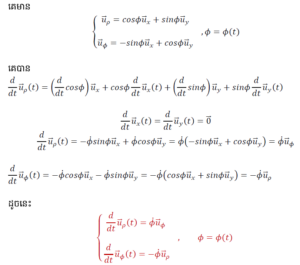
តម្រុយស្វ៊ែ

ឯកសារយោង

薩摩順吉：物理の数学，岩波書店，1995,pp.91-95, 101-107