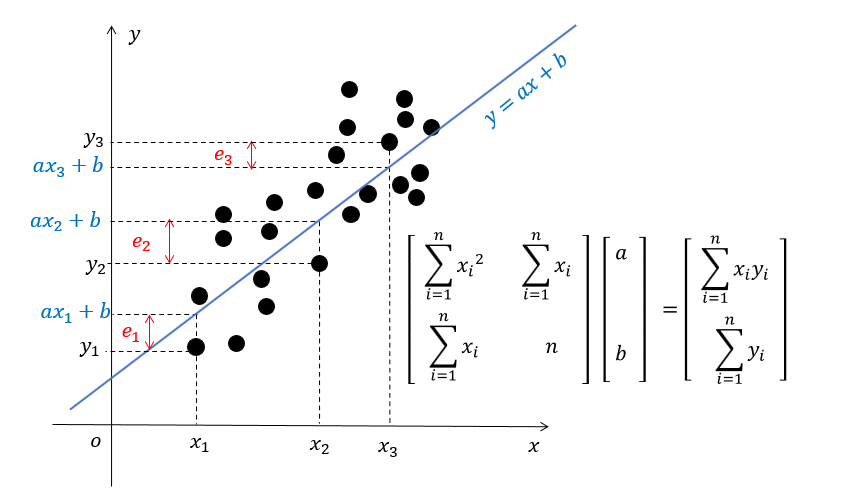
យើងមានទិន្នន័យចំនួន n នៃអញ្ញាតិពីរ (xi, yi) , i=1;n ដែល x គឺជាអញ្ញតិឯករាជ្យ(មិនអាស្រ័យ)(independent variable) ហើយ y គឺជាអញ្ញតិអាស្រ័យ(dependent variable)។ មានន័យថា y អាស្រ័យនឹង x បើ x ប្រែប្រួលនោះ y ក៏ប្រែប្រួលដែរ។ យើងអាចដៅចំណុចនៃអញ្ញតិទាំងពីរបានក្នុងប្លង់ដេកាតដូចរូបខាងក្រោម(រូបភាពទី១)
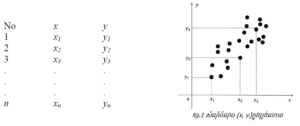
តម្រែតម្រង់(regression) គឺជាម៉ូដែលស្ថិតិ(statistical model) មួយដែលត្រូវបានប្រើដើម្បីស្វែងរកឬបង្កើតទំនាក់ទំនងរវាងអញ្ញតិឯករាជ្យ និងអញ្ញតិអាស្រ័យតាមរយៈទិន្នន័យដែលមាន។ នៅក្នុងតម្រែតម្រង់លីនែអ៊ែ(linear regression)យើងសន្មតថាទំនាក់ទំនងនេះជាទំនាក់ទំនងលីនែអ៊ែ ហើយតម្រែតម្រង់លីនែអ៊ែធម្មតា(simple linear regression) គឺជាតម្រែតម្រង់លីនែអ៊ែដែលមានអញ្ញតិឯករាជ្យតែមួយគត់។ ដូចនេះយើងអាចសរសេរទំនាក់ទំនងរវាងអញ្ញតិទាំងពីរបានក្រោមទម្រង់លីនែអ៊ែដូចខាងក្រោម។ នៅទីនេះ a, b ជាប៉ារ៉ាម៉ែតដែលយើងនឹងគណនាដោយប្រើប្រាស់ទិន្នន័យដែលមានស្រាប់។
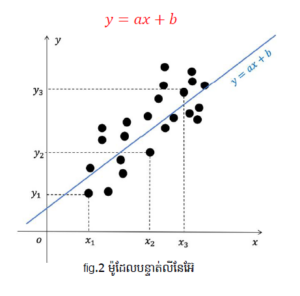
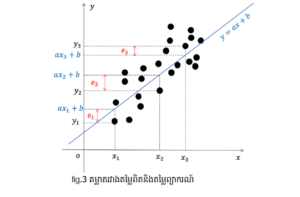
(xi, yi )ជាទិន្នន័យដែលមានស្រាប់(តម្លៃពិត)។ បើយើងជំនួស xi ណាមួយក្នុងសមីការ y = ax+b យើងនឹងបានតម្លៃ axi+b ដែលតម្លៃនេះជាគ្រាន់តែជាតម្លៃព្យាករណ៍តែប៉ុណ្ណោះ។ ដើម្បីដឹងថាការព្យាករណ៍និងការពិតខុសគ្នាកម្រិតណាយើងត្រូវគណនាកម្រិតល្អៀង(error)របស់វា។ យក e ជាកម្រិតល្អៀងរវាង yi និង axi+b នោះ e អាចសរសេរដូចខាងក្រោម (រូបភាពីទី៣)
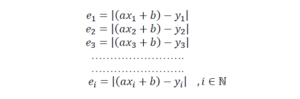
តាមរូបកម្រិតល្អៀង ei ក៏ជាចម្ងាយរវាង់ពីរចំណុច (xi , yi) ទៅ (xi , axi+b) ដូចនេះកម្រិតល្អៀងគឺ

កម្រិតល្អៀង ei ជាទំហំមិនថេរ ប្រែប្រួលតាមទិន្នន័យនីមួយៗដែលផ្តល់ឲ្យ។ ដូចនេះកម្រិតល្អៀងដែលកើតចេញពីទិន្នន័យទាំងអស់ត្រូវតែជាផលបូកកម្រិតល្អៀងនីមួយៗចូលគ្នា។ បើយើងតាង f ជាអនុគមន៍កម្រិតល្អៀងនោះ f គឺជាផលបូកកម្រិតល្អៀងចូលគ្នា ពោលគឺ f អាចសរសេរក្រោមទម្រង់ដូចខាងក្រោម។
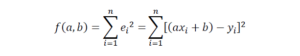
តម្លៃព្យាករណ៍ដែលល្អបំផុតគឺជាតម្លៃព្យាករណ៍ដែលស្រដៀងឬដូចតម្លៃពិត មានន័យថាកម្រិតល្អៀងត្រូវតែតិចបំផុត។ ដូចនេះយើងអាចរកតម្លៃប៉ារ៉ាមែត a, b បានតាមរយៈលក្ខខណ្ឌតម្លៃអប្បបរិមានៃ f
លក្ខខណ្ឌតម្លៃអប្បបរិមានៃ f គឺ
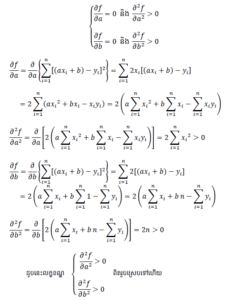
លក្ខខណ្ឌដើម្បីបានអប្បបរិមានៃ f នៅសល់តែពីរទេគឺ
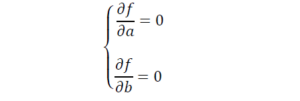

ដូចនេះប៉ារ៉ាមែត a, b អាចកំណត់បានដូចខាងក្រោម
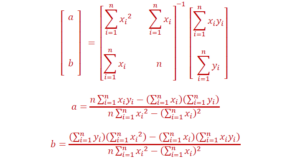
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/