អាំងតេក្រាលខ្សែ Line Integral

*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ​​ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា

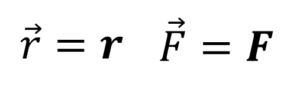
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ​ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។

សេចក្តីផ្តើម

នៅបបឋមសិក្សាយើងធ្លាប់រៀនគណនាក្រលាផ្ទៃដែលនេះគឺជាសញ្ញាណដំបូងនៃអាំងតេក្រាល។

នៅវិទ្យាល័យយើងធ្លាប់រៀនអាំងតេក្រាលដើម្បីឲ្យយល់ពីនិយមន័យនិងចេះចាំលក្ខណៈពិសេសរបស់វា។ អាំងតេក្រាលកម្រិតមធ្យមសិក្សា គឺជាអាំងតេក្រាលនៃអនុគមន៍ស្កាលែមានមួយអថេរf(x) ហើយជាទូទៅគេចំណាំថាវាជាក្រលាផ្ទៃនៃអ្វីមួយ Area = ∫f(x)dx ។ ការយល់បែបនេះជាការត្រឹមត្រូវតែវាមិនមែនជាអត្ថន័យទាំងស្រុងនោះទេ។ ក្នុងការអនុវត្តជាក់ស្តែងដូចជាក្នុងរូបវិទ្យា និងវិស្វកម្មជាដើមអាំងតេក្រាលមានន័យទូលំទូលាយនិងមានលក្ខណៈពិសេសជាច្រើន។ ដូចជាអនុគមន៍ដែលត្រូវធ្វើអាំងតេក្រាលជាដើម បន្ថែមពីលើអនុគមន៍ស្កាលែក៏មានអាំងត្រកាលនៃអនុគមន៍វ៉ិចទ័រដែរ(កម្មន្តនៃកម្លាំងក្រៅ…)។​ បើយើងគិតអំពីចលនាក្នុងលំហ ដែនកំណត់នៃអាំងតេក្រាលមិនមានជាចំណុចនឹងថេរពីរនោះទេ តែគេត្រូវគិតពីគន្លងនៃចលនាទៅវិញ។ បើគិតពីលក្ខណៈរូប(Physical Property)នៃបាតុភូតនីមួយៗ អាំងតេក្រាលមានបីប្រភេទគឺ អាំងតេក្រាលខ្សែ(Line Integral) អាំងតេក្រាលផ្ទៃ(Surface Integral) និងអាំងតេក្រាលមាឌ(Volume Integral)។ អាំងតេក្រាលនីមួយៗសុទ្ធតែអាចគណនាបានចំពោះអនុគមន៍ស្កាលែ និងអនុគមន៍វ៉ិចទ័រ ហើយលក្ខណៈនិងអត្ថន័យរបស់វាមានភាពប្លែកៗគ្នា។

អត្ថបទខាងក្រោមនេះទាក់ទងនឹងអាំងតេក្រាលខ្សែផ្តោតសំខាន់លើលក្ខណៈនៃដែនវ៉ិចទ័រដូចជាដែនកម្លាំង និងដែនលំហូរនៃសន្ទនីយ៍ជាដើម។

អាំងតេក្រាលខែ្សនៃដែនស្កាលែ Line Integral of a Scalar Field

ដូចនៅក្នុងមេរៀនប្រវែងធ្នូឬចម្ងាយចរក្នុងទំព័រមួយផ្សេងទៀត(សូមចុចត្រង់នេះដើម្បីមើលមេរៀនប្រវែងធ្នូ) យកប្រវែងធ្នូ s ជាប៉ារ៉ាមែត តាមនិយមន័យ អាំងតេក្រាលខ្សែ(Line Integral)តាម(លើ)ខ្សែកោង C ក្នុងដែនស្កាលែ f(x , y , z) គឺ

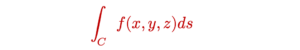
អាចនិយាយបានថាប្រវែងធ្នូ s គឺជា​អាំងតេក្រាលខ្សែក្នុងករណីដែលតម្លៃដែនស្កាលែ(បរិមាណស្កាលែ) f ត្រង់ចំណុចនីមួយៗស្មើនឹង1ថេរ។ ដោយឡែកអាំងតេក្រាលខ្សែដែលយើងសិក្សាត្រង់នេះ ដូចបង្ហាញក្នុងរូបខាងក្រោម គឺជាករណីដែលដែនស្កាលែ f មានតម្លៃប្រែប្រួលតាមទីតាំង នៅតាមបំណែងចែកអង្កត់តូចៗ Δs នីមួយៗគេគុណតម្លៃដែនស្កាលែ f នឹង Δs ហើយបូកតម្លៃនេះបញ្ចូលគ្នាលើខ្សែកោង C ទាំងស្រុង។ ខ្សែកោង C ប្រៀបដូចជាដែនកំណត់នៃអាំងតេក្រាល។

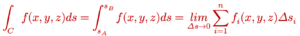
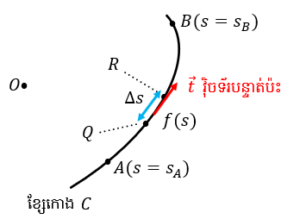
នេះមានន័យថា តាមរយៈអាំងតេក្រាលខ្សែ គេអាចទទួលបានលក្ខណៈពិសេសនៃខ្សែកោង C ទាំងស្រុងដោយគិតបញ្ចូលទាំងលក្ខណៈពិសេសតាមទីតាំងនីមួយៗ(បរិមាណស្កាលែ)។ ឧទាហរណ៍ ចំពោះសីតុណ្ហភាពដែលជាបរិមាណស្កាលែ f ប្រែប្រួលតាមទីតាំង(x, y, z) បើគេវាស់សីតុណ្ហភាពពីទីតាំង A ទៅ B ពេលកំពុងធ្វើដំណើរ នោះតម្លៃនៃអាំងតេក្រាលខ្សែនឹងក្លាយជាសន្ទស្សន៍កម្តៅ(កម្រិតក្តៅ)លើផ្លូវ C ទាំងស្រុង។  

ខ្សែកោង C ក្នុងដែនស្កាលែ f(x, y, z) កំណត់ដោយវ៉ិចទ័រទីតាំង r ដែល

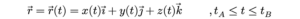
ដូចនៅក្នុងមេរៀនប្រវែងធ្នូដែរ

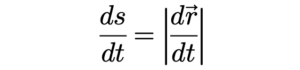
គេបានអាំងតេក្រាលខ្សែកំណត់ដោយប៉ារ៉ាមែត t គឺ

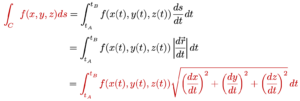
ឧទាហរណ៍ ចំពោះដែនស្កាលែ f(x,y,z) = 2xy + z³ ខ្សែកោង C កំណត់ដោយប៉ារ៉ាមែត t គឺ r=(t, t, t) (0 ≤ t≤ 1) ចូរគណនា

ចម្លើយគម្រូ

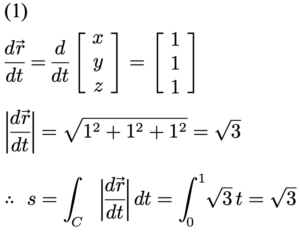
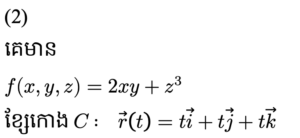
ខ្សែកោង C ជាគន្លងស្ថិតក្នុងដែនស្កាលែ f ដូចនេះសមីការខ្សែកោង C ត្រូវផ្ទៀងផ្ទាត់ក្នុងដែនស្កាលែ f ពោលគឺ

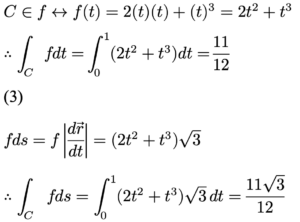
ក្នុងការគណនាអាំងតេក្រាលខ្សែ ប្រសិនបើខ្សែកោង C ជាគន្លងចាប់ផ្តើមពី A ឆ្ពោះទៅកាន់ B នោះគន្លងបញ្ច្រស(ពីចំណុច B ទៅ A)គឺជាខ្សែកោង -C ពោលគឺ

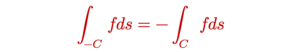
ម្យ៉ាងទៀតប្រសិនបើខ្សែកោង C ជាខ្សែកោងដែលកើតចេញពីតំណខ្សែផ្សេងគ្នា C₁ និង C₂ នោះគេអាចពន្លាតអាំងតេក្រាលខ្សែបានគឺ(C = C₁+C₂)

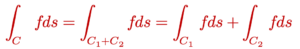
ឧទាហរណ៍​ ចំពោះដែនស្កាលែ f(x,y,z) = 2xy + z³ ចូរគណនាអាំងតេក្រាលខ្សែ ∫fdt តាមខ្សែកោង C ដូចខាងក្រោម

(1) ខ្សែកោង C : ជាខ្សែត្រង់ចេញពីគល់តម្រុយទៅចំណុច​ A(3, 2, 1)

(2) ខ្សែកោង C : ជាខ្សែត្រង់ចេញពីគល់តម្រុយទៅចំណុច​ B(2, 0, 0)​ រួចចេញទៅចំណុច A(3, 1, 2)

ចម្លើយគម្រូ

(1)

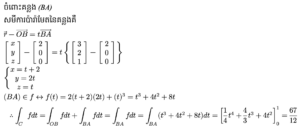
អាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ  Line Integral of a Vector Field

ដូចអាំងតេក្រាលខ្សែនៃដែនស្កាលែលើគន្លង C ដែរ យើងក៏អាចគណនាអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័របានដែរ។​ គន្លងខ្សែកោង C ក្នុងដែនវ៉ិចទ័រ​ v = ui+vj+wk​ អាចសរសេរជាវ៉ិចទ័រទីតាំងដែលមានប្រវែងធ្នូ s ជាប៉ារ៉ាមែតគឺ​ r = r(s) = x(s)i + y(s)j + z(s)k , s ∈ [A, B] ហើយវ៉ិចទ័របន្ទាត់ប៉ះឯកតា(Unit Tangent Vector)គឺ t = dr/ds (សូមចុចត្រង់នេះដើម្បីមើលមេរៀនវ៉ិចទ័របន្ទាត់ប៉ះ)

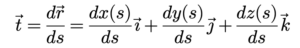
តាមនិយមន័យអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ v តាមគន្លងខ្សែកោង C (តាមទិសបន្ទាត់ប៉ះ)គឺ

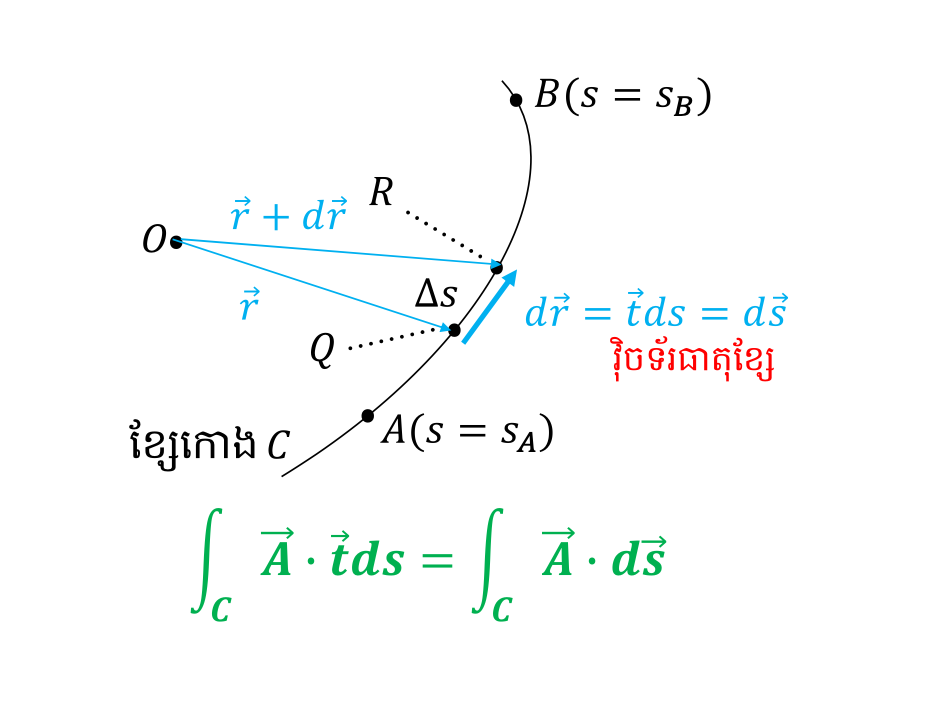
អាំងតេក្រាលនេះ ដូចបង្ហាញក្នុងរូបខាងក្រោម គឺជាផលបូកបញ្ចូលគ្នានៃកំប៉ូសង់នៃដែនវ៉ិចទ័រ v ដែលស្របនឹងខ្សែកោង C (ដែលតាងដោយវ៉ិចទ័របន្ទាត់ប៉ះឯកតា t ) តាមបណ្តោយធ្នូទាំងស្រុង។​ ឧទាហរណ៍ ករណី v ជាវ៉ិចទ័រកម្លាំងក្រៅនៃសន្ទនីយ៍ ហើយខ្សែកោង C គឺជាគន្លងនៃចលនារបស់រូបធាតុពីចំណុច​ A ទៅ B  អាំងតេក្រាលនេះនឹងក្លាយជា បរិមាណកម្មន្តសរុបដែលទទួលបានពីកម្លាំងតាមទិសបន្លាស់ទី v · t ។ សូមប្រយ័ត្នកុំច្រលំប៉ារ៉ាមែត t នឹង វ៉ិចទ័របន្ទាត់ប៉ះឯកតា t ។

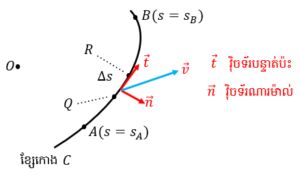
ម្យ៉ាងទៀតយក n ជាវ៉ិចទ័រណរម៉ាល់ឯកតា( Unit Normal Vector) នៃខ្សែកោង C នោះអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ v តាមទិសកែងនឹងគន្លងខ្សែកោង C គឺ

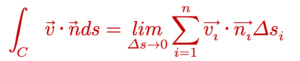
អាំងតេក្រាលនេះគឺជាផលបូកបញ្ចូលគ្នានៃកំប៉ូសង់ដែនវ៉ិចទ័រ v ដែលកែងនឹងខ្សែកោង C ​(ពោលគឺv · n ) ។ ឧទាហរណ៍ ករណី v ជាវ៉ិចទ័រល្បឿននៃសន្ទនីយ៍ នោះអាំងតេក្រាលនេះគឺជា បរិមាណលំហូរសរុបនៃសន្ទនីយ៍កាត់ទទឹងក្នុងចន្លោះចំណុច A ទៅ B លើខ្សែកោង C ។  

 

ឧទាហរណ៍ ចំពោះវ៉ិចទ័រទីតាំង r មានណម​ r  ដែនវ៉ិចទ័រ v = r/r³ ដូចរូបខាងក្រោម គន្លង​ C ចេញពីចំណុច P→ Q→ R ចូរគណនាអាំងតេក្រាលខ្សែខាងក្រោម

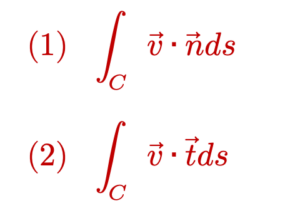
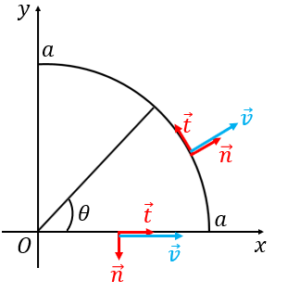
ចម្លើយគម្រូ

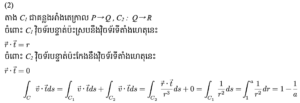
អាំងតេក្រាលខ្សែនៃផលគុណស្កាលែរវាងវ៉ិចទ័រ A=(A_x, A_y, A_z) លើខ្សែចំនុចនៃខ្សែកោង​ C  នឹងវ៉ិចទ័បន្ទាប់ប៉ះឯកតា t គឺ

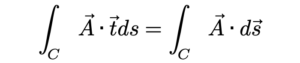
tds = ds ហៅថាវ៉ិចទ័រធាតុខ្សែ(Line Element Vector) ដែលសម្គាល់លក្ខណៈពិសេសរបស់ខ្សែ។ ដូចក្នុងរូបខាងក្រោម វ៉ិចទ័រធាតុខ្សែ ds គឺជាគម្លាតរវាងវ៉ិចទ័រទីតាំង r+dr ត្រង់ R នឹង វ៉ិចទ័រទីតាំង r ត្រង់ Q ។ ដោយវ៉ិចទ័រទីតាំង r=(x, y, z) ហេតុនេះវ៉ិចទ័រទីតាំងនៃ ds គឺ

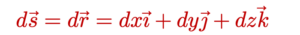
ខ្សែកោង C ជាអនុគមន៍នៃប៉ារ៉ាមែត t

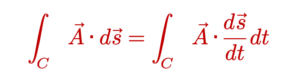
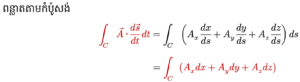
នេះគឺជាផលបូកអាំងតេក្រាលខ្សែលើគន្លង C ទាក់ទងនឹងកំប៉ូសង់នីមួយៗនៃដែនវ៉ិចទ័រ A

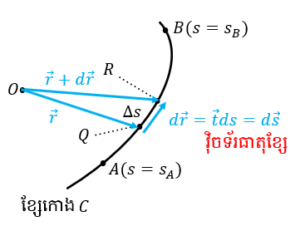
ឧទាហរណ៍ ចំពោះដែនវ៉ិចទ័រ A = (x²y, y², xyz) ហើយគន្លងខ្សែកោង C កំណត់ដោយវ៉ិចទ័រទីតាំង r = (t, t, t) ដែល t ∈  [0,1] ។ គណនាអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ A តាមគន្លង C ។

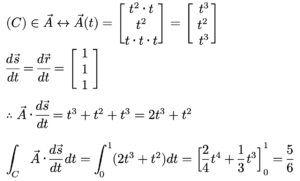
នៅក្នុងមេកានិចអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ F គឺជាកម្មន្តនៃដែនកម្លាំង F មានអំពើលើអង្គធាតុធ្វើឲ្យវាផ្លាស់ទីលើគន្លង C ។ សូមចុចលើតំណភ្ជាប់ខាងក្រោមដើម្បីមើលមេរៀននោះ។

អនុវត្តអាំងតេក្រាលខ្សែក្នុងរូបវិទ្យា

លំហាត់អនុវត្ត

ចំពោះដែនវ៉ិចទ័រ​ A = (xy , yz , zx) គន្លង C ជាខ្សែត្រង់ចាប់ពីចំណុច (1, 2, 3 )​​ ដល់ចំណុច (3, 4, 1)។

ចូរគណនាអាំងតេក្រាលខ្សែនៃដែនវ៉ិចទ័រ A លើគន្លង C​​ ។

ចម្លើយគម្រូ

ឯកសារយោង

薩摩順吉：物理の数学，岩波書店，1995, pp.107-111