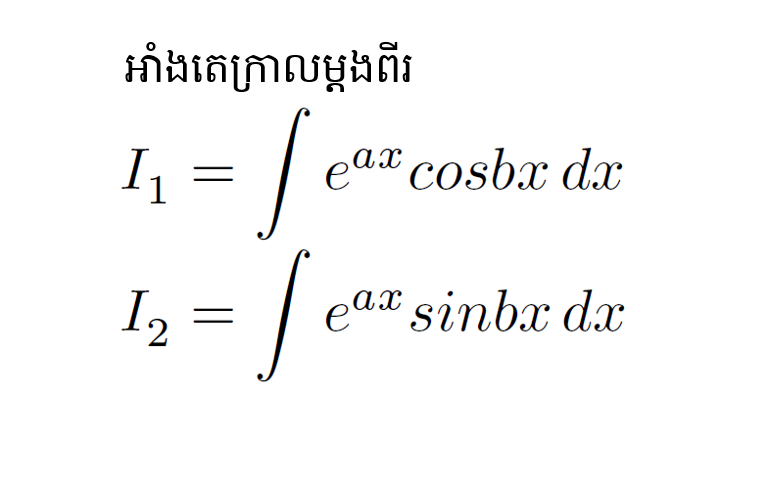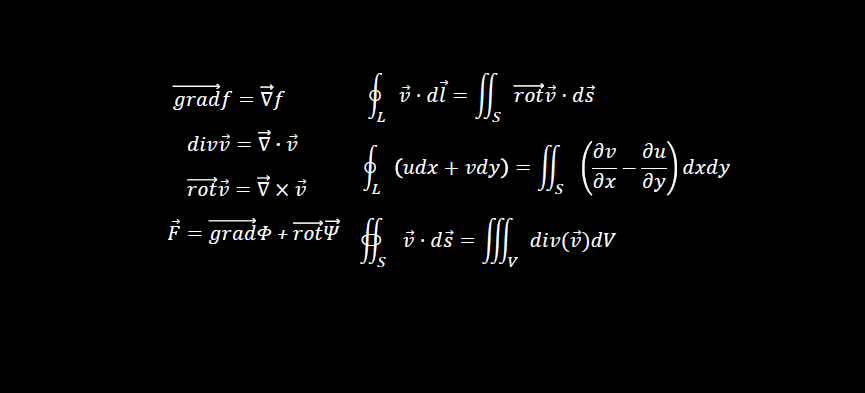*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា
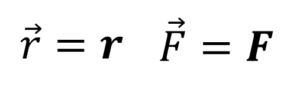
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។
ទ្រឹស្តីបទHelmholtz
ចំពោះដែនវ៉ិចទ័រ A ប្រសិនបើមានដែនស្កាលែ f ណាមួយដែលផ្ទៀងផ្ទាត់ទំនាក់ទំនងខាងក្រោម
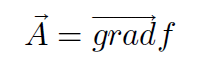
នោះគេថា f គឺជាប៉ូតង់ស្យែលស្កាលែ( Scalar Potential) ឬប៉ូតង់ស្យែលនៃ A ។ លក្ខខណ្ឌចាំបាច់ដើម្បីឲ្យដែនវ៉ិចទ័រ A មានប៉ូតង់ស្យែលស្កាលែ f គឺ
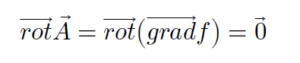
ដែលមានន័យថាដែនវ៉ិចទ័រ A គឺជាដែនមានបន្សាយតែគ្មានរង្វិល។
ដោយឡែក ចំពោះដែនវ៉ិចទ័រ A ប្រសិនបើមានដែនវ៉ិចទ័រ B ណាមួយដែលផ្ទៀងផ្ទាត់ទំនាក់ទំនងខាងក្រោម
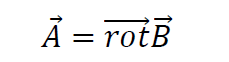
នោះគេថា ដែនវ៉ិចទ័រ B គឺជាប៉ូតង់ស្យែលវ៉ិចទ័រ(Vector Potential)នៃ A ។ លក្ខខណ្ឌចាំបាច់ដើម្បីឲ្យដែនវ៉ិចទ័រ A មានប៉ូតង់ស្យែលវ៉ិចទ័រ B គឺ
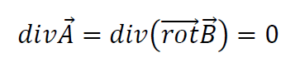
ដែលមានន័យថាដែនវ៉ិចទ័រ A គឺជាដែនវិលតែគ្មានបន្សាយ។
ជាទូទៅ ចំពោះដែនវ៉ិចទ័រ A ដែលជាលំហូរមិនវិល (rotA=0) ហើយជាលំហូរគ្មានបន្សាយ(divA=0) គេអាចសរសេរ A ជាទម្រង់ផលបូកនៃប៉ូតង់ស្យែលស្កាលែ និងប៉ូតង់ស្យែលវ៉ិចទ័រដូចខាងក្រោម
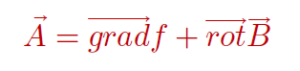
រូបមន្តនេះហៅថាទ្រឹស្តីបទHelmholtz
រូបមន្តនេះត្រូវបានអនុវត្តចំពោះបាតុភូតទាំងឡាយណាដែលទាក់ទងនឹងដែន។ នៅក្នុងរូបវិទ្យា វាក៏ជារូបមន្តមួយសំខាន់ដែរ។ ចំពោះការអនុវត្តខ្លះៗក្នុងរូបវិទ្យាលោកអ្នកអាចពិនិត្យមើលតំណភ្ជាប់នៃមេរៀនរូបវិទ្យាខាងក្រោម។
ការអនុវត្តទ្រឹស្តីបទទ្រឹស្តីបទHelmholtzក្នុងរូបវិទ្យា។
លំហូរខ្យល់ក្នុងប្លង់ដេកពីរវិមាត្រ
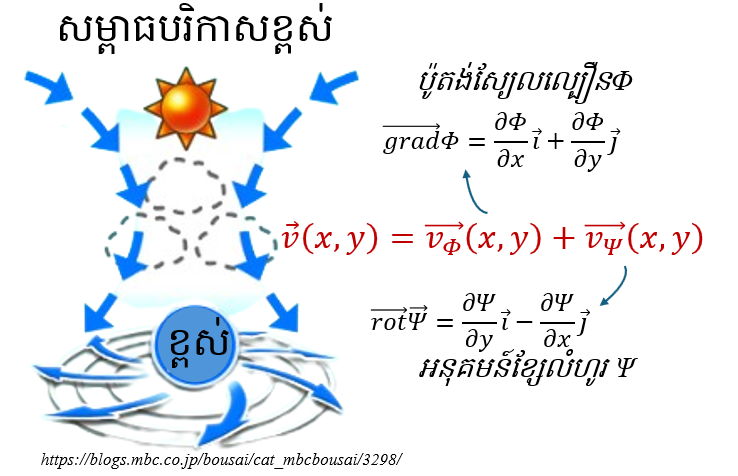
ការអនុវត្តមួយនៃទ្រឹស្តីបទ Helmholtz គឺការសិក្សាពីឧតុនិយម(Meteorology) និងវារីសាស្ត្រ (Hydraulics)។ អនុវត្តទ្រឹស្តីបទនេះចំពោះលំហូរខ្យល់ក្នុងប្លង់ដេកពីរវិមាត្រនោះគេបាន
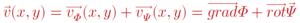
Φ(x,y)ហៅថាប៉ូតង់ស្យែលល្បឿន(Velocity Potential)ដែលត្រូវជាប៉ូតង់ស្យែលស្កាលែ។ ចំណែកឯΨ(x,y)=(0, 0, Ψ(x,y)) ហៅថាអនុគមន៍ខ្សែលំហូរ(Flow Line Function)ដែលត្រូវជាប៉ូតង់ស្យែលវ៉ិចទ័រ។ នេះមានន័យថាដែនលំហូរពីរវិមាត្រ v អាចសរសេរជាផលបូករវាងលំហូ vΦ ដែលកំណត់ដោយប៉ូតង់ស្យែលល្បឿន Φ នឹងលំហូរ vΨ ដែលកំណត់ដោយអនុគមន៍ខ្សែលំហូរ Ψ ។
កំប៉ូសង់នៃលំហូរ vΦ គឺ
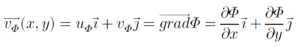
កំប៉ូសង់នៃលំហូរ vΨ គឺ
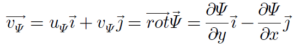
រង្វិលនៃលំហូរ vΦ ដែលកំណត់ដោយប៉ូតង់ស្យែលល្បឿន Φ គឺ (រង្វិលជុំវិញអ័ក្ស z)
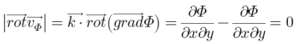
នេះមានន័យថា gradΦ គឺជាលំហូរមានបន្សាយចេញចូលតែគ្មានរង្វិល។ បន្សាយនៃលំហូរនេះគឺ
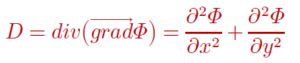
ដែលមានន័យថាវាត្រូវបានកំណត់ដោយប៉ូតង់ស្យែលល្បឿន Φ ។
ដោយឡែក បន្សាយនៃលំហូរ vΨ ដែលកំណត់ដោយអនុគមន៍ខ្សែលំហូរ Ψ គឺ
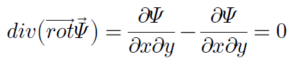
នេះមានន័យថា rotΨ ជារង្វិលដែលគ្មានបន្សាយ។ ស្ថានភាពរង្វិល ζ (vorticity) តាមអ័ក្សរឈរ(អ័ក្សរង្វិលz)គឺ
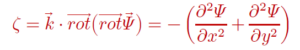
ដែលមានន័យថាវាត្រូវបានកំណត់ដោយអនុគមន៍ខ្សែលំហូ Ψ ។
ដើម្បីឲ្យ rotΨ ក្លាយជាលំហូគ្មានភាពវិលវល់ (vorticity) លុះត្រាតែស្ថានភាពរង្វិល ζ តាមទិសឈរត្រូវស្មើសូន្យពោលគឺ
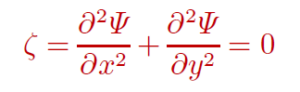
នេះជាសមីការឡាផ្លាស(Laplace Equation) ហេតុនេះអនុគមន៍ខ្សែលំហូ Ψ គឺជាអនុគមន៍អាកម៉ូនិច(Harmonic Function)។ ម្យ៉ាងទៀត ដើម្បីឲ្យ gradΦ ក្លាយជាលំហូរដែលគ្មានបន្សាយលុយត្រាតែ D = 0 មានន័យថា
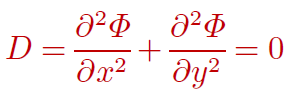
ដែលនេះក៏ជាសមីកាឡាផ្លាសដែរ។ ហេតុនេះប៉ូតង់ស្យែលល្បឿន Φ ក៍ជាអនុគមន៍អាកម៉ូនិច។
ដូចបង្ហាញក្នុងរូបខាងក្រោម នៅប៉ូលខាងជើងចំពោះទីតាំងសម្ពាធខ្ពស់(នៅជិតផែនដី)ជាទូទៅលំហូរខ្យល់នៅទីនោះជាលំហូដែលវិលឡើងលើតាមទិសទ្រនិចនាឡិកា។ លំហូរពីរវិមាត្រ v បែបនេះ ដូចក្នុងរូបខាងក្រោម តែងតែត្រូវកំណត់ដោយផលបូករវាង ទី១លំហូរគ្មានរង្វិល(មានបន្សាយ) vΦ ដែលគណនាចេញពីប៉ូតង់ស្យែលល្បឿន Φ នឹងទី២លំហូរគ្មានបន្សាយ(មានរង្វិល) vΨ ដែលកំណត់ដោយអនុគមន៍ខ្សែលំហូរ Ψ ។ លំហូរដែលគ្មានរង្វិល(មានបន្សាយ) vΦ មានទិសកែងនឹងខ្សែតម្លៃថេរ(isoline)នៃប៉ូតង់ស្យែលល្បឿន Φ ។ ចំណែកឯលំហូរដែលគ្មានបន្សាយ(មានរង្វិល) vΨ បក់ស្របនឹងខ្សែតម្លៃថេរនៃអនុគមន៍ខ្សែលំហូរ Ψ ។

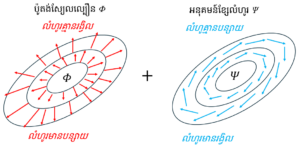
តាមរយៈសមីការខាងលើ ប្រសិនបើយើងស្គាល់ពីបន្សាយ D យើងអាចកំណត់ប៉ូតង់ស្យែលល្បឿន Φ បានដោយគ្រាន់តែផ្តល់នូវលក្ខខណ្ឌព្រំដែន (Boundary Conditions) នៃសមីការឌីផេរ៉ង់ស្យែល។ ដូចគ្នាដែរប្រសិនបើយើងស្គាល់កំប៉ូសង់ទិសឈរនៃស្ថានភាពរង្វិល ζ យើងក៏អាចកំណត់អនុគមន៍ខ្សែលំហូរ Ψ បានដោយគ្រាន់តែផ្តល់លក្ខខណ្ឌព្រំដែននៃសមីការឌីផេរ៉ង់ស្យែល។ ហេតុនេះយើងអាចនិយាយបានថា ដែនលំហូរ v អាចកំណត់បាន(ឬប្រែប្រួលអាស្រ័យនឹង)ដែនស្កាលែពីរគឺ បន្សាយ D និងទិសឈរនៃស្ថានភាពរង្វិល ζ ។
លំហាត់អនុវត្ត
(1) ចំពោះដែនស្កាលែ f = -x2y + z2 គណនា A = gradf ។ ម្យ៉ាងទៀត បញ្ជាក់ថា f ជាប៉ូតង់ស្យែលស្កាលែនៃ A ដោយបង្ហាញថា rotA = 0 ។
(2) ចំពោះដែនវ៉ិចទ័រ B = (-yz-xy2z , -x2yz ) គណនា A = rotB។ ម្យ៉ាងទៀត បញ្ជាក់ថា B គឺជាប៉ូតង់ស្យែលវ៉ិចទ័រនៃ A ដោយបង្ហាញថា divA=0 ។
ចម្លើយគម្រូ

ឯកសារយោង
- 薩摩順吉:物理の数学,岩波書店,1995, pp.100-101
- 頭痛ーる 気圧予報で体調管理,気象に関する気象用語,低気圧、高気圧とは、その定義や違い,13/Apr/2024 updated, 13/Apr/2024 Accesed : https://zutool.jp/column/glossary/low-pressure_high-pressure
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/