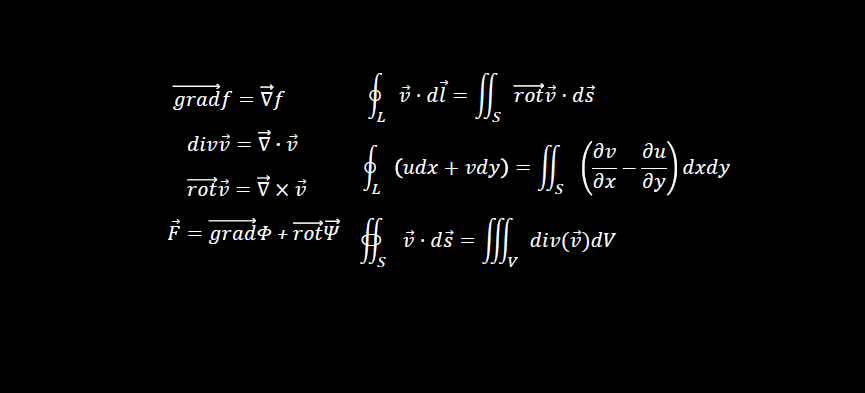រង្វិលនៃដែនវ៉ិចទ័រ Rotation(Curl) of a Vector Field

*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ​​ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា

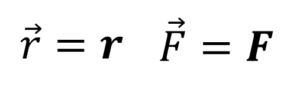
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ​ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។

============================

បើយើងគិតពីលំហូរនៃសន្ទនីយ៍លើផ្ទៃក្នុងប្លង់ដេក ល្បឿនលំហូរពីរវិមាត្រមានកំប៉ូសង់ពីរគឺកំប៉ូសង់ស្របនឹងអង្កត់នៃផ្ទៃ និងកំប៉ូសង់កែងនឹងអង្កត់នៃផ្ទៃ។​​ កំប៉ូសង់កែងនឹងអង្កត់នៃផ្ទៃបង្កើតបានជាបន្សាយ(Divergence) ដែលបង្ហាញពីលក្ខណៈផុសចេញឬស្រូបចូលនៃសន្ទនីយ៍។ ចំណែកឯកំប៉ូសង់ល្បឿនលំហូរដែលស្របនឹងអង្កត់នៃផ្ទៃ បង្កើតបានជាចលនារង្វិលដែលត្រូវបានកំណត់ដោយទំនាក់ទំនងគណិតវិទ្យាមួយហៅថា​រង្វិល(curl, rotation) កើតចេញពីផលគុណរវាងសញ្ញាណដេរីវេណាប្លា∇គុណនឹងដែនវ៉ិចទ័រ(ល្បឿន)។​

និយមន័យ

ដើម្បីសម្រួលដល់ការសិក្សាយើងនឹងពិនិត្យមើលដែនល្បឿនសន្ទនីយ៍ពីរវិមាត្រ

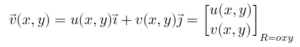
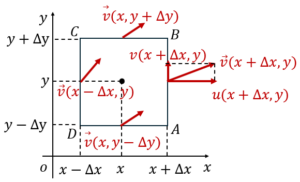
យើងនឹងពិនិត្យចលនាចេញចូលនៃសន្ទនីយ៍ក្នុងផ្ទៃ ABCD (ផ្ចិត(x,y))ក្នុងប្លង់ដេក(xy)ដែលប្រវែងតាមអ័ក្សដេកគឹ 2Δx ហើយប្រវែងតាមអ័ក្សឈរគឺ 2Δy។ វ៉ិចទ័រល្បឿនលំហូរប្រែប្រួលតាមទីតាំងនីមួយៗ។ ត្រង់ចំណុចកណ្តាលអង្កត់ AB គឺv(x+Δx, y) ត្រង់ចំណុចកណ្តាល BC គឺv(x, y+Δy) ត្រង់ចំណុចកណ្តាល CD គឺv(x-Δx, y)  ត្រង់ចំណុចកណ្តាល DA គឺv(x, y-Δy)។ ដោយសារវាជាសន្ទនីយ៍ពីរវិមាត្រ ដូចនេះដែនល្បឿនលំហូរគ្មានកំប៉ូសង់តាមទិសដែលកែងនឹងប្លង់ (xy) (ទិស z)នោះទេ។ យើងអាចសរសរកំប៉ូសង់ត្រង់ទីតាំងនីមួយៗតាមវ៉ិចទ័រដូចខាងដូចខាងក្រោម

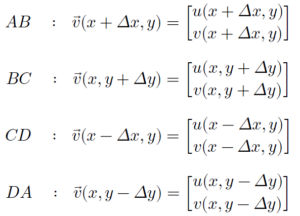
ក្នុងការគណនាបន្សាយ(Divergence)ពោលគឺចលនាចេញចូលនៃសន្ទនីយ៍ក្នុងផ្ទៃ ABCD កំប៉ូសង់ដែលត្រូវគិតគឺកំប៉ូសង់តាមទិសកែងនឹងអង្កត់នីមួយៗ។ មានន័យថាកំប៉ូសង់ស្របអាចចោលបាន។ ផ្ទុយទៅវិញ​ ពេលនេះយើងសិក្សាពីរង្វិលនៃសន្ទនីយ៍ក្នុងផ្ទៃ ABCD ហេតុនេះកំប៉ូសង់ដែលចាំបាច់ត្រូវគិតគឺកំប៉ូសង់តាមទិសស្របនឹងអង្កត់​​ ហើយកំប៉ូសង់កែងអាចចោលបាន។ កំប៉ូសង់ល្បឿនលំហូរតាមអង្កត់នីមួយៗដែលត្រូវគិតមានដូចខាងក្រោម

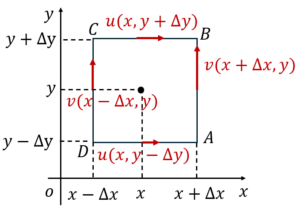
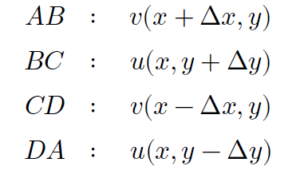
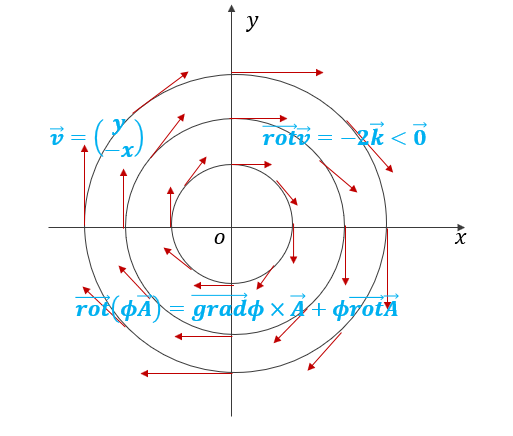
សន្មតយកទិសផ្ទុយទ្រនិចនាឡិកា A→​ B→​​​ C→ D ជាទិសវិជ្ជមាននៃល្បឿនមុំ(=ល្បឿនរង្វិល/កាំរង្វិល)។ ចំពោះអង្កត់ AB ល្បឿនមុំω_AB បានមកពី កំប៉ូសង់ស្រប(នឹងអង្កត់នេះ)នៃវ៉ិចទ័រល្បឿនលំហូរ v(x+Δx, y)​ ចែកនឹងកាំΔx ។ ដូចគ្នាដែរចំពោះអង្កត់ផ្សេងទៀតល្បឿនមុំនីមួយៗគឺ

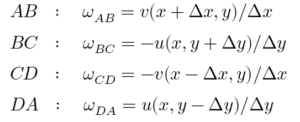
អង្កត់ BC និង CD មានសញ្ញាដកដោយសារវាជារង្វិលស្របតាមទ្រនិចនាឡិកាដែលជាទិសអវិជ្ជមាន(សញ្ញាព្រួយក្រហមក្នុងរូបខាងលើ)។ មធ្យមនៃល្បឿនមុំω លើផ្ទៃ ABCD ទាំងស្រុងគឺ

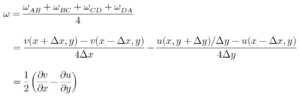
យើងឃើញថាតម្លៃនេះជាបរិមាណដែលបង្ហាញពីរង្វិលនៃសន្ទនីយ៍ជុំវិញអ័ក្សដែលកែងនឹងប្លង់(xy)ពោលគឺអក្ស័ z ។ ដោយទំហំ 1/2 គ្រាន់តែជាប៉ារ៉ាម៉ែតស្កែល(Scale Parameter​ ប៉ារ៉ាម៉ែតទាក់ទងនឹងទំហំឬបរិមាណ) យើងអាចមិនគិតវាបាន។ ចំពោះដែនវ៉ិចទ័របីវិមាត្រ v = ui + vj + wk គេត្រូវគិតរង្វិលជុំវិញអ័ក្សនីមួយៗដូចជា x, y, z ពោលគឺគេត្រូវគិតរង្វិលជាបីវិមាត្រ។

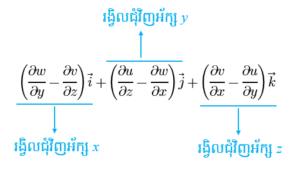
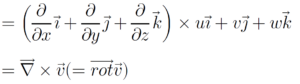
ផលគុណខ្វែងរវាងណាប្លានឹងដែនវ៉ិចទ័រនេះហៅថារង្វិលនៃដែនវ៉ិចទ័រ។ ដោយក្នុងភាសាអង់គ្លេសគេប្រើពាក្យ rotation ឬ curl ទើបនិមិត្តសញ្ញារង្វិលគឺ rot​ ឬ curl ។ ក្នុងវែបសាយនេះយើងប្រើតែ rot ទេ។ វិធីគុណនេះអាចសរសេរជាដេទែមីណង់ដូចខាងក្រោម

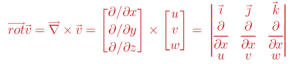
តម្លៃរង្វិលនៃដែនវ៉ិចទ័រ​ v គឺជាស្ថានភាពរង្វិល(ទិសដៅនិងទំហំឬភាពខ្លាំង)នៃសន្ទនីយ៍ពេលយើងពិនិត្យត្រង់ផ្នែងតូចបំផុតណាមួយ(microscopic)។

ឧទាហរណ៍ទី១

គណនាកំប៉ូសង់រង្វិល z នៃដែនវ៉ិចទ័រពីរវិមាត្រខាងក្រោម

ចម្លើយគម្រូ

(1)

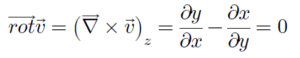
ដែនវ៉ិចទ័រជាដែនគ្មានរង្វិល។ ដូចរូបភាពខាងក្រោមដែនវ៉ិចទ័រ v =xi+yj ជាដែនសាយចេញពីគល់តម្រុយមានទម្រង់ដូចការបញ្ចេញរស្មី(radiation) ដូចនេះវាគ្មានរង្វិលទេ។

(2)

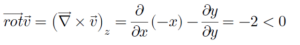
ដែន​ v គឺជារង្វិលតាមទិសដៅអវិជ្ជមាន(ស្របទ្រនិចនាឡិកា)។ ដូចបង្ហាញក្នុងរូបខាងក្រោមរ v =yi – xj ជាដែនវិលស្របទ្រនិចនាឡិកាមានគល់តម្រុយជាផ្ចិតរង្វិល។

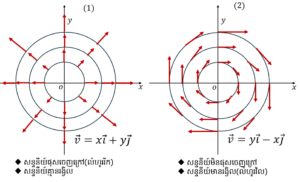
លក្ខណៈគ្រឹះនៃរង្វិលនៃដែនវ៉ិចទ័រ

ចំពោះដែនវ៉ិចទ័រ A, B ដែនស្កាលែ φ មេគុណថេរ α, β គេបានទំនាក់ទំនងដូចខាងក្រោម

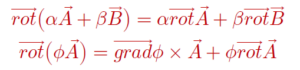
បំណកស្រាយ តាង A = A_xi+A_yj+A_zk     B = B_xi+B_yj+B_zk

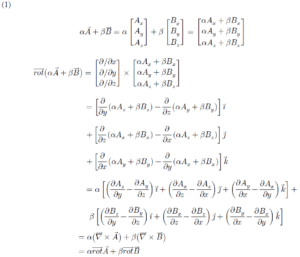
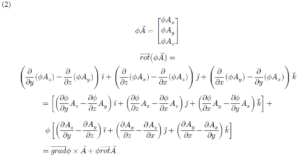
ឧទាហរណ៍ទី២

ចំពោះដែនវ៉ិចទ័រ A = (xy, y²z, -xyz²) ដែនស្កាលែ φ = x²+yz ចូរគណនាតម្លៃខាងក្រោម

 

 

 

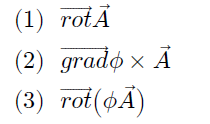
ចម្លើយគម្រូ

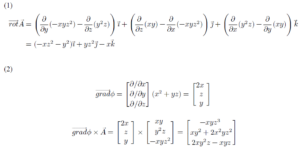
(3) តាមរូបមន្តយើងអាចប្រើចម្លើយ (1) និង (2)

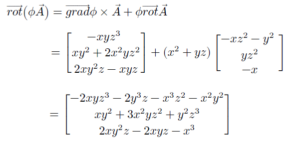
លំហាត់អនុវត្ត

1/ គណនារង្វិលនៃដែនវ៉ិចទ័រខាងក្រោម

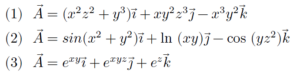
2/ ចំពោះវ៉ិចទ័រទីតាំង r = (x, y, z) , r = (x²+y²+z²)^1/2 ​​ ចូរគណនារង្វិលខាងក្រោមជាអនុគមន៍នៃ r និង r

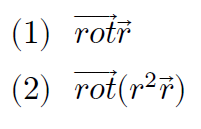
ចម្លើយគម្រូ

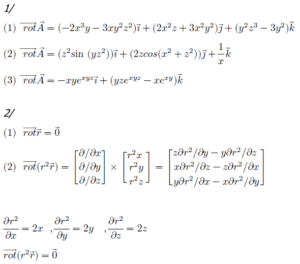
ឯកសារយោង

薩摩順吉：物理の数学，岩波書店，1995, pp.96-99