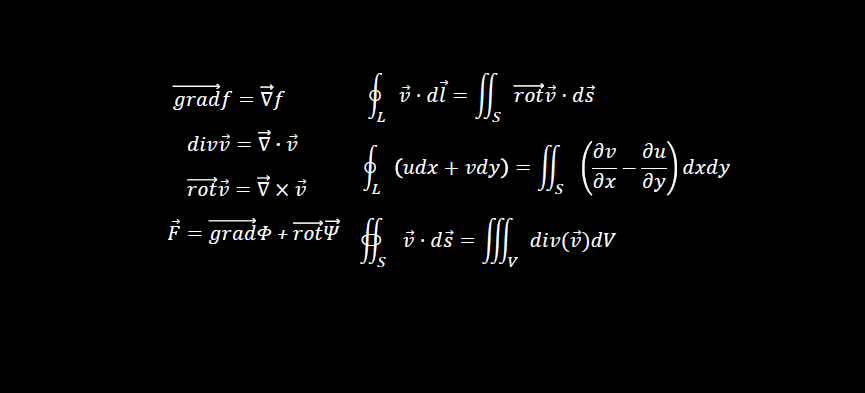*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា
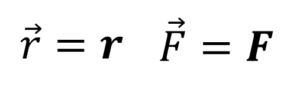
ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។
=============================
បាតុភូតរូបដូចជាដែនកម្លាំំងក្រៅដែលធ្វើឲ្យចំណុចរូបធាតុមានបន្លាស់ទីបង្កើតបានជាកម្មន្ត។ គេអាចគណនាកម្មន្តដោយប្រើអាំងតេក្រាលខ្សែ(Line Integral)ដែលមានគន្លង(ខ្សែ)ជាដែនកំណត់នៃអាំងតេក្រាល។ ដូចគ្នាដែរករណីភ្លុច(Flux)ដែលជាចំនួនខ្សែដែននៃទំហំវ៉ិចទ័រឆ្លងកាត់ផ្ទៃណាមួយ អាចគណនាបានដោយប្រើអាំងតេក្រាលផ្ទៃ(Surface Integral)។ លក្ខណៈរូប(Physical Property)នៃផ្ទៃដែលដែនវ៉ិចទ័រឆ្លងកាត់គឺជាដែនកំណត់នៃអាំងតេក្រាលបែបនេះ។
អាំងតេក្រាលផ្ទៃនៃដែនស្កាលែ
វ៉ិចទ័រណរម៉ាល់នៃផ្ទៃកោង Normal Vector of Surface
ចំពោះវ៉ិចទ័រទីតាំងនៃចំណុចដែលប្រែប្រួលដោយប៉ារ៉ាមែត t មួយ គេអាចគូខ្សែកោង C បានដោយធ្វើបម្រែបម្រួល t ។ ចុះករណីចំណុចប្រែប្រួលដោយប៉ារ៉ាមែត 2 ផ្សេងគ្នាតើគេវានឹងទៅជាយ៉ាងណា?
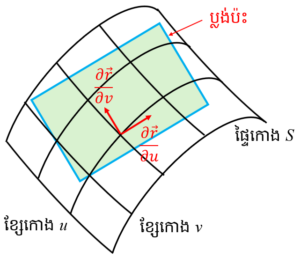
ចំពោះចំណុចដែលកើតឡើងដោយប៉ារ៉ាមែត u, v ពីរ តាមរយៈការធ្វើបម្រែបម្រួលប៉ារ៉ាមែត្រទាំងពីរដាច់ដោយឡែកពីគ្នាគេនឹងទទួលបានផ្ទៃកោង (Surface)។ ផ្ទៃកោង S កំណត់ដោយវ៉ិចទ័រទីតាំង
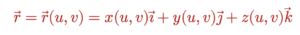
ដោយបង្ហាញក្នុងរូបខាងក្រោម វ៉ិចទ័រទីតាំង r ដែលបង្ហាញពីផ្ទៃកោង S គឺ បង្កើតបានខ្សែកោងu កាលណាគេធ្វើឲ្យ u ប្រែប្រួលដោយទុក v ឲ្យនៅថេរដដែល។ ផ្ទុយទៅវិញគេនឹងទទួលបានខ្សែកោងv កាលណា v ប្រែប្រួលហើយ u នៅថេរ។ វ៉ិចទ័របន្ទាត់ប៉ះ(Tangent Vector) នៃខ្សែកោងនីមួយៗគឺ ∂r/∂u និង ∂r/∂v ។ នៅត្រង់ចំណុចមួយដែលវ៉ិចទ័របន្ទាត់ប៉ះទាំងពីរ ∂r/∂u និង ∂r/∂v បង្កើតបានប្លង់ដេកគេហៅថាប្លង់ប៉ះ(Tangent Plan) ដែលប៉ះនឹងផ្ទៃកោង S ត្រង់ចំណុចនោះ។ ម្យ៉ាងទៀតផលគុណខ្វែងនៃវ៉ិចទ័រ ∂r/∂u នឹង ∂r/∂v គឺជាវ៉ិចទ័រណរម៉ាល់ (Normal Vector)នៃប្លង់ដេកប៉ះ ដូចនេះវ៉ិចទ័រណរម៉ាល់ប្លង់ប៉ះឯកតា(Unit Tangent Plan Vector) n គឺ
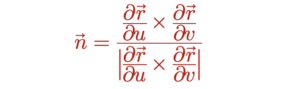
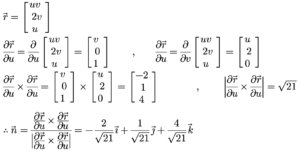
ឧទាហរណ៍ ចំពោះផ្ទៃកោង S ដែលកំណត់ដោយ r = uvi + 2vj + uk ចូរគណនាវ៉ិចទ័រណរម៉ាល់ឯកតា n នៃផ្ទៃ S ។
ចម្លើយគម្រូ
ក្រលាផ្ទៃនៃផ្ទៃកោង Area of Surface
តទៅទៀតយើងនឹងគិតអំពីក្រលាផ្ទៃនៃផ្ទៃកោង S ។ ផ្ទៃកោង S កំណត់ដោយវ៉ិចទ័រទីតាំង r ដែលកំណត់ដោយប៉ារ៉ាមែត u, v ។ ដូចបង្ហាញក្នុងរូបភាពខាងក្រោម យើងនឹងគិតអំពីផ្ទៃកោងតូច PQRT ដែលហ៊ុំព័ទ្ធដោយ Δu, Δv ដែលកើតចេញពីបម្រែបម្រួលខ្សែកោង u និងខ្សែកោង v ត្រង់ទីតាំងណាមួយ។ ផ្ទៃតូច PQRT អាចចាត់ទុកជាប្រលេឡូក្រាម(តម្លៃប្រហែល)បាន។ ត្រង់នេះ ប្រលេឡូក្រាមមានជ្រុងឈមគ្នាពីរគឺ PT = (∂r/∂u)Δu និង PQ = (∂r/∂v)Δv ។ ដោយទំហំនៃផលគុណខ្វែងរវាងវ៉ិចទ័រពីរបង្កើតបានជាក្រលាផ្ទៃនៃប្រលេឡូក្រាម ក្រឡាផ្ទៃតូចបំផុតនៃប្រលេឡូក្រាម PQRT គឺជាទំហំផលគុណខ្វែងនៃវ៉ិចទ័រ PT នឹង PQ ។
ដូចនេះក្រឡាផ្ទៃ S ក្នុងដែនកំណត់ D ណាមួយ ដែលកើតចេញពីផលបូកផ្ទៃតូច Δs លើប្លង់ uv គឺ

ឧទាហរណ៍ គណនាក្រលាផ្ទៃ S នៃផ្ទៃកោង r = ui + vj +(1-u-v)k ក្នុងដែន D : 0 ≤ u ≤ 1, 0 ≤ v ≤ 1
ចម្លើយគម្រូ
អាំងតេក្រាលផ្ទៃនៃដែនស្កាលែ Surface Integral of a Scalar Field
យើងសង្កេតឃើញថា ក្រលាផ្ទៃនៃផ្ទៃកោង S គឺជាអាំងតេក្រាលនៃវ៉ិចទ័រទីតាំង r ដែលបង្កើតផ្ទៃកោង S គុណនឹងតម្លៃថេរ(ស្មើ 1)ត្រង់ទីតាំងនីមួយៗ។ មានន័យថា ចំពោះដែនស្កាលែ f(x,y,z)ដែលមានផ្ទៃកោង S អាស្រ័យនៅ តម្លៃ f(x,y,z) = k (k ≠ 0) ថេរ មិនប្រែប្រួលតាមទីតាំង ករណី k=1 អាំងតេក្រាលនៃវ៉ិចទ័រទីតាំងនៃផ្ទៃកោងគឺជាក្រលាផ្ទៃ។ លំនាំនេះគឺដូចគ្នានឹងការគណនាប្រវែងធ្នូដែរ ដែលជាអាំងតេក្រាលខ្សែ(សូមចុចទីនេះដើម្បីមើលមេរៀនប្រវែងធ្នូ)។ តទៅទៀតយើងនឹងគិតអំពីអាំងតេក្រាលចំពោះផ្ទៃកោង S នៃដែនស្កាលែ f ណាមួយដែលទាក់ទងនឹងមេគុណនៃទីតាំងនីមួយៗ។ ផ្ទៃកោង S កំណត់ដោយប៉ារ៉ាមែត u, v ហើយចំពោះដែនកំណត់ D ក្នុងប្លង់ uv គេបាន
ទំនាក់ទំនងនេះហៅថាអាំងតេក្រាលផ្ទៃនៃដែនស្កាលែ។
ឧទាហរណ៍ ចំពោះដែនស្កាលែ f(x, y, z) = x+2y+z ផ្ទៃកោង S : x+y+z=2 (0 ≤ x ≤ 1, 0 ≤ y ≤ 1, z ≥ 0)ចូរគណនាអាំងតេក្រាលផ្ទៃ ∫∫fdS។
ចម្លើយគម្រូ
តាងប៉ារ៉ាមែត u, v ដោយ u=x, v=y នោះ z = 2-u-v
វ៉ិចទ័រទីតាំងនៃផ្ទៃកោង S គឺ

អាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រ Surface Integral of a Vector Field
អាំងតេក្រាលខ្សែតាមខ្សែកោងមានពីរគឺ អាំងតេក្រាលខ្សែចំពោះដែនស្កាលែ និងអាំងតេក្រាលខ្សែចំពោះដែនវ៉ិចទ័រ។ ដូចគ្នាដែរ អាំងតេក្រាលផ្ទៃក៏ចែកចេញជាពីរដែរ គឺអាំងតេក្រាលផ្ទៃនៃដែនស្កាលែ និងអាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រ។
ដូចបង្ហាញក្នុងរូបខាងក្រោម ផ្ទៃកោង S ជាផ្ទៃកោងក្នុងលំហបីវិមាត្រ ហើយយើងនឹងសិក្សាអំពីបរិមាណសន្ទនីយ៍សរុបដែលហូរកាត់ទទឹងផ្ទៃកោងដោយដែនលំហូរ v = ui + vj+ wk ។ យក n ជាវ៉ិចទ័រណរម៉ាល់ឯកតាដែលកែងនឹងធាតុផ្ទៃកោង(Surface Element)ក្នុងផ្ទៃកោង S ។ កំប៉ូសង់ល្បឿននៃសន្ទនីយ៍ដែលហូរចេញពីធាតុផ្ទៃ ΔS គឺ
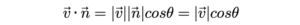
ដោយបរិមាណលំហូរដែលហូរចេញពីធាតុផ្ទៃ ΔS គឺជាផលគុណរវាងក្រលាផ្ទៃនឹងល្បឿនលំហូរ
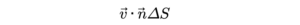
ដូចនេះបរិមាណលំហូរសរុបនៃសន្ទនីយ៍ដែលកាត់ទទឹកផ្ទៃកោង S គឺ
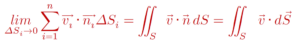
នេះគឺជាអាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រ v កាត់តាមផ្ទៃកោង S ។ dS = ndS ហៅថាវ៉ិចទ័រធាតុផ្ទៃ។ នេះមានន័យថា អាំងតេក្រាលផ្ទៃ គឺជាអាំងតេក្រាលនៃផលគុណស្កាលែរវាងដែនវ៉ិចទ័រ v នឹងវ៉ិចទ័រណរម៉ាល់ឯកតា n ។
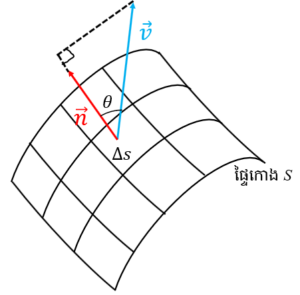
វ៉ិចទ័រណរម៉ាល់អាចកំណត់ដោយមុំតាមអ័ក្សនីមួយៗដូចខាងក្រោម
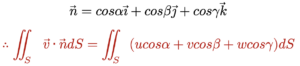
ម្យ៉ាងទៀត រូបភាពនៃធាតុផ្ទៃ ΔS លើប្លង់yz, zx ,xy រៀងគ្នាគឺ cosαΔS = ΔyΔz , cosβΔS = ΔxΔz . cosγΔs = ΔxΔy

ឧទាហរណ៍ ផ្ទៃស្វ៊ែ S មានកាំ a មានផ្ទិតត្រង់គល់តម្រុយ។ យកវ៉ិចទ័រទីតាំង r មានណម r ចូរគណនាអាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រ v = r/r3 ។
ចម្លើយគម្រូ
វ៉ិចទ័រទីតាំង r មានទិសកែងនឹងផ្ទៃស្វ៊ែ S ជានិច្ច។ ដូចនេះវ៉ិចទ័រណរម៉ាល់ឯកតានៃផ្ទៃកោង S គឺ n = r/r ។ ម្យ៉ាងទៀតដោយ r∙r=r2 គេបាន
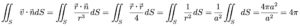
នេះមានន័យថា អាំងតេក្រាលផ្ទៃមិនអាស្រ័យនឹងកាំនៃស្វ៊ែនោះទេ។
អាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រដែលយើងបានសិក្សាកន្លងមកនេះ
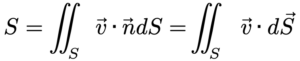
ជាតម្លៃស្កាលែដោយសារវាជាអាំងតេក្រាលនៃផលគុណស្កាលែរវាងដែនវ៉ិចទ័រ v នឹង វ៉ិចទ័រណរម៉ាល់ឯកតា n ។ ដោយឡែក ចំពោះដែនវ៉ិចទ័រ v នៅក្នុងទំនាក់ទំនងខាងក្រោម
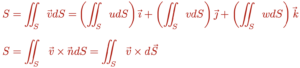
ក៏ជាអាំងតេក្រាលផ្ទៃនៃដែនវ៉ិចទ័រដែរ។ ចូរប្រយ័ត្នត្រង់ថាករណីនេះចម្លើយនៃអាំងតេក្រាលគឺជាទំហំវ៉ិចទ័រ។
ឧទាហរណ៍ ចំពោះដែនវ៉ិចទ័រ A = 2xi + yj +3zk ផ្ទៃ S : x + y + z = 1 (x ≥ 0 , y ≥ 0 , z ≥ 0) ចូរគណនាអាំងតេក្រាលផ្ទៃ S = ∫∫A∙ndS ។
ចម្លើយគម្រូ
តាងប៉ារ៉ាមែត u, v ដោយ u=x, v=y នោះ z = 1-u-v
វ៉ិចទ័រទីតាំងនៃផ្ទៃកោង S គឺ

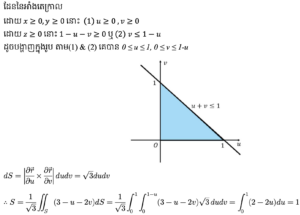
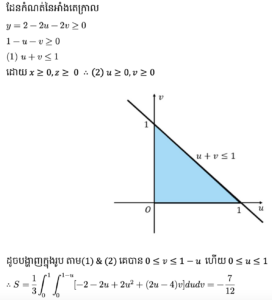
លំហាត់អនុវត្ត
ចំពោះដែនវ៉ិចទ័រ

ចម្លើយគម្រូ

ឯកសារយោង
薩摩順吉:物理の数学,岩波書店,1995, pp.107-111
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/