*កំណត់ចំណាំ : មានរបៀបពីរយ៉ាងដើម្បីសរសេរវ៉ិចទ័រ។ គេអាចប្រើសញ្ញាព្រួញ ឬអក្សរដិត។ឧទាហរណ៍ដូចជា

ក្នុងវែបសាយនេះយើងប្រើប្រាស់ទាំងពីរទម្រង់។ សញ្ញាព្រួញសម្រាប់សមីការ ឬរូបមន្តវែងៗ រីឯនិមិត្តសញ្ញាគណិតវិទ្យាខ្លីៗដែលមាននៅក្នុងអត្ថបទឬល្បះសម្រាប់ពន្យល់យើងប្រើអក្សរដិតវិញ។
សេចក្តីផ្តើម
កម្មន្ត (Work) នៃដែនវ៉ិចទ័រ(Vector Field) អាចគណនាបានតាមអាំងតេក្រាលខ្សែ(Line Integral)។ ករណីខ្សែ(គន្លង)ជាខ្សែបើកការគណនាអាំងតេក្រាលខ្សែមិនពិបាកទេ។ បញ្ហាគឺនៅពេលខ្សែជាខ្សែបិទ(Closed Line)ដែលជាព្រំដែន(Boundary)នៃផ្ទៃណាមួយ។ ក្នុងករណីនេះ ការគណនាអាំងតេក្រាលខ្សែមានភាពស្មុគស្មាញនិងចំណាយពេលច្រើន ហេតុនេះគេច្រើនជំនួសវាដោយអាំងតេក្រាលផ្ទៃ(Surface Integral)ដែលមានភាពងាយស្រួលជាង។ ការភ្ជាប់ទំនាក់ទំនងរវាងអាំងតេក្រាលខ្សែនិងអាំងតេក្រាលផ្ទៃហៅថាទ្រឹស្តីបទStokes។
លោក George Green(ចក្រភពអង់គ្លេស) ជាគណិតវិទូដែលគ្មានការអប់រំផ្លូវការម្នាក់។ លោកបានចេញផ្សាយឯកសារស្រាវជ្រាវរបស់លោកក្នុងឆ្នាំ1828ដែលក្នុងនោះមានរូបមន្តមួយដែលក្រោយមកគេស្គាល់ថាជាទ្រឹស្តីGreenនៃប្លង់ដេក។ ជាអកុសលការចេញផ្សាយនេះពុំត្រូវបានគេទទួលស្គាល់ទេ។ ក្រោយលោកទទួលអនិច្ចកម្ម មានសាស្ត្រាចារ្យនៅសាកលវិទ្យាល័យCambridgeម្នាក់ឈ្មោះWilliam Thomson(Lord Kelvin) (ចក្រភពអង់គ្លេស)បានស្វែងយល់់ពីសារៈសំខាន់នៃឯកសាររបស់លោក Green ក៏បានបោះពុម្ពឡើងវិញនៅឆ្នាំ1845។ ពេលនោះកិត្តនាមរបស់Greenក៏កើតមានឡើង។
Kelvin បានជួប George Gabriel Stokes(អៀកឡង់) នៅ Cambridge ហើយអ្នកទាំងពីរបានចាប់អារម្មណ៍ជាខ្លាំងលើកិច្ចការរបស់ Green។ ការពិតមុនពេលជំនួបនេះកើតឡើង Kelvin បានរកឃើញថានៅក្នុងទ្រឹស្តីបទ Green មានទំនាក់ទំនងសំខាន់មួយដែលក្រោយមកគេស្គាល់វាថាជាទ្រឹស្តីបទStokes។ ទ្រឹស្តីបទStokesចេញជារូបរាងឡើងដំបូងនៅក្នុងសំបុត្រមួយច្បាប់ដែល Kelvinបានផ្ញើទៅឲ្យ Stokes ក្នុងឆ្នាំ 1850 ។ នៅឆ្នាំ1854 Stokesបានដាក់ទ្រឹស្តីដែលគាត់និងKelvin រកឃើញនៅក្នុងវិញ្ញាសារប្រលងឲ្យសិស្សរបស់គាត់បកស្រាយ។ គេមិនដឹងថាមានអ្នកស្រាយចេញឬអត់ទេនៅពេលនោះ។ តែយ៉ាងណាក៏ដោយហេតុការណ៍នេះធ្វើឲ្យគេហៅទ្រឹស្តីនេះថាទ្រឹស្តីបទStokesជាប់រហូតមកដល់សព្វថ្ងៃ។ ក្រោយមកក្នុងឆ្នាំ1861លោកHermann Hakel(អាល្លឺម៉ង់)ជាមនុស្សដំបូងគេដែលបានបកស្រាយទ្រឹស្តីបទStokeដោយគិតទៅលើចលនានៃសន្ទនីយ៍។
ខាងក្រោមនេះជាមូលដ្ឋានគ្រឹះមួយចំនួនដែលអ្នកសិក្សាដំបូងគួរស្វែងយល់ទាក់ទងនឹងទ្រឹស្តីបទStokes និងទ្រឹស្តីបទ Green នៃប្លង់ដេក។
និយមន័យនិងបំណកស្រាយ
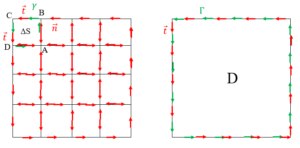
យើងនឹងសិក្សាលើរង្វិលនៃសន្ទនីយ៍ក្នុងផ្ទៃចតុកោណABCDដែលមានផ្ចិត (x, y) ប្រវែងជ្រុងដេកនិងជ្រុងឈរ 2Δx=2Δy=Δs ដូចបង្ហាញក្នុងរូបខាងក្រោម។ ដែនល្បឿនលំហូរ v ជាដែនពីរវិមាត្រកំណត់ដោយ v = ui + vj ។ (សម្រាប់ការអធិប្បាយបន្ថែមសូមមើលមេរៀនរង្វិលដោយចុចត្រង់នេះ)
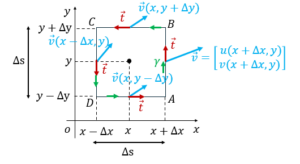
ដោយចលនារង្វិលទាក់ទងតែទៅនឹងកំបូសង់ស្របនឹងអង្កត់នីមួយៗនៃផ្ទៃ ABCD ហេតុនេះតម្លៃមធ្យមនៃល្បឿនមុំក្នុងផ្ទៃទាំងមូលគឺ (ដើម្បីសម្រួលឲ្យងាយយល់យើងយក 8ΔxΔy = 2Δs)
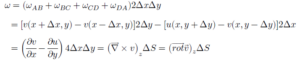
ល្បឿនមុំតាមអង្កត់នីមួយៗអាចសរសេរតាមផលគុណស្កាលែដូចខាងក្រោម
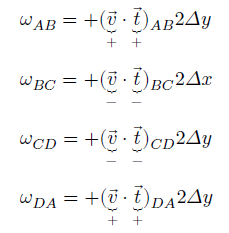
ដែល t គឺជាវ៉ិចទ័របន្ទាត់ប៉ះឯកតានៃអ័ក្សនីមួយ។ យកទិសច្រាសទ្រនិចនាឡិការជាទិសវិជ្ជមាននៃរង្វិលហើយរងិ្វលផ្តើមចេញពី A → C → D ហើយត្រលប់មក A វិញ។ ទិសដៅនៃល្បឿនមុំតាមអង្កត់នីមួយៗគឺ
ចំពោះអង្កត់ AB
ល្បឿនលំហូរ v មានទិសស្របនឹងទិសវិជ្ជមាននៃអ័ក្ស y ដែលជាទិសវិជ្ជមាននៃរង្វិល មានន័យថា v មានទិសវិជ្ជមាន។ វ៉ិចទ័របន្ទាត់ប៉ះ t ក៏មានទិសស្របនឹងទិសវិជ្ជមាននៃអ័ក្ស y ដែរមានន័យថា t មានទិសវិជ្ជមាន។ ហេតុនេះល្បឿនមុំωAB ត្រូវមានសញ្ញាវិជ្ជមាន(បូក×បូក)។
ចំពោះអង្កត់ BC
ល្បឿនលំហូរ v មានទិសស្របតាមទិសអវិជ្ជមាននៃអ័ក្ស x ដែលជាទិសអវិជ្ជមាននៃរង្វិល មានន័យថា v មានទិសអវិជ្ជមាន។ វ៉ិចទ័របន្ទាត់ប៉ះ t ក៏មានទិសដូច v ដែរមានន័យថា t មានទិសអវិជ្ជមាន។ ហេតុនេះល្បឿនមុំωBC ត្រូវមានសញ្ញាវិជ្ជមាន(ដក×ដក)។
ចំពោះអង្កត់ CD
ល្បឿនលំហូរ v មានទិសស្របនឹងទិសអវិជ្ជមាននៃអ័ក្ស y ដែលជាទិសអវិជ្ជមាននៃរង្វិល មានន័យថា v មានទិសអវិជ្ជមាន។ វ៉ិចទ័របន្ទាត់ប៉ះ t ក៏មានទិសដូច v ដែរមានន័យថា t មានទិសអវិជ្ជមាន។ ហេតុនេះល្បឿនមុំωCD ត្រូវមានសញ្ញាវិជ្ជមាន(ដក×ដក)។
ចំពោះអង្កត់ DA
ល្បឿនលំហូរ v មានទិសស្របនឹងទិសវិជ្ជមាននៃអ័ក្ស x ដែលជាទិសវិជ្ជមាននៃរង្វិល មានន័យថា v មានទិសវិជ្ជមាន។ វ៉ិចទ័របន្ទាត់ប៉ះ t ក៏មានទិសដូច v ដែរមានន័យថា t មានទិសវិជ្ជមាន។ ហេតុនេះល្បឿនមុំωCD ត្រូវមានសញ្ញាវិជ្ជមាន(បូក×បូក)។
នេះមានន័យថា បើយើងសរសរជាទម្រង់ផលគុណស្កាលែ នោះចំពោះអង្កត់ទាំងអស់ល្បឿនមុំមានសញ្ញាវិជ្ជមានជានិច្ច។ ហេតុនេះល្បឿនមុំខាងលើអាចសរសេរដូចខាងក្រោម
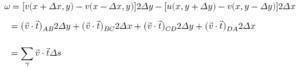
ដែល 2Δx=2Δy=Δs
នេះគឺជាផលបូកស៊េរីនៃតួនីមួយៗគិតតាមរង្វិលច្រាសទ្រនិចនាឡិកា។ គន្លងរង្វិលមួយជុំនេះតាងដោយ γ (ព្រួញពណ៌បៃតង)។ ដោយល្បឿនមុំអាចសរសរជាទម្រង់រង្វិលបាន(ចុចនៅទីនេះដើម្បីមើលមេរៀនរង្វិល)ដូចនេះ
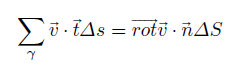
ដែល n គឺជាវ៉ិចទ័រណរម៉ាល់ឯកតាដែលកែងនឹងផ្ទៃΔS
ក្នុងលំហបីវិមាត្ររង្វិលនៃដែនលំហូរ v គឺ
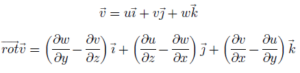
ជាបន្តទៅទៀតយើងនឹងគិតពីផ្ទៃដែន D ធំមួយដែលកើតចេញពីសំណុំផ្ទៃចតុកោណតូចៗ ΔS (ABCD) ដូចក្នុងរូបខាងក្រោម។ ព្រួញពណ៌ក្រហមគឺជាវ៉ិចទ័របន្ទាត់បះឯកតាដែលវិលតាមទិសច្រាសទ្រនិចនាឡិកា។ យើងឃើញថា ចំពោះអង្កត់ពីរត្រួតគ្នា វ៉ិចទ័របន្ទាត់ប៉ះមានទិសផ្ទុយគ្នាដែលមានន័យថាត្រង់នេះផលបូកវ៉ិចទ័រទាំងពីរស្មើសូន្យ។ ហេតុនេះចំពោះដែន D គន្លងចាំបាច់ដែលត្រូវគិតពីរងិ្វល(v∙tΔs)គឺមានតែគន្លងខាងក្រៅបង្អស់ ( Γ ) តែប៉ុណ្ណោះ។ យើងអាចពង្រីកផលបូកនៃសមីការខាងលើពីផ្ទៃតូច ΔS ទៅជាផ្ទៃធំ D បានដូចខាងក្រោម
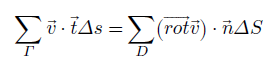
អនុវត្តលីមីតΔs→ 0, ΔS→ 0 យើងបាន
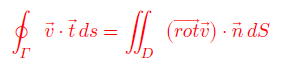
ទំនាក់ទំនងនេះហៅថាទ្រឹស្តីបទStokes។ ដោយប្រើធាតុខ្សែ tds =ds និងធាតុផ្ទៃ ndS = dS យើងបានទ្រឹស្តីបទStokesអាចសរសេរ
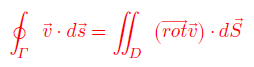
ទ្រឹស្តីនេះជាការភ្ជាប់ទំនាក់ទំនងរវាងអាំងតេក្រាលខ្សែ(អង្គខាងឆ្វេង)នឹងអាំងតេក្រាលផ្ទៃ(អង្គខាងស្តាំ)។
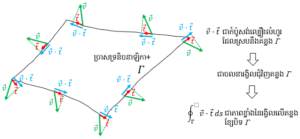
អត្ថន័យនៃអង្គខាងឆ្វេង ( ∫v∙tds )enclosed
គឺជាអាំងតេក្រាល v∙t លើខ្សែបិទ Γ នៃដែន D ។ ដោយv∙tds គឺជាកំប៉ូសង់នៃ v ដែលស្របនឹងគន្លង Γ ត្រង់ទីតាំងនីមួយៗ គុណថែមនឹងប្រវែងធ្នូតូច ds ដូចនេះអាំងតេក្រាលនេះជាអាំងតេក្រាលភាពខ្លាំងនៃលំហូរដែលវិលតាមខ្សែបិទ Γ ។ បើលំហូរខ្លាំងតាមទិសច្រាសទ្រនិចនាឡិកានោះវាជាលំហូរវិជ្ជមាន បើលំហូរខ្លាំងតាមទិសស្របទ្រនិចនាឡិកានោះវាជាលំហូរអវិជ្ជមាន។
អត្ថន័យនៃអង្គខាងស្តាំ ∫∫(rotv)∙nds
ជាការគណនាអាំងតេក្រាលផ្ទៃលើដែន D នៃកំប៉ូសង់រង្វិល rotv តាមទិសកែងនឹងដែន D។ តាមនិយមន័យរង្វិលគឺជាបរិមាណវ៉ិចទ័រដែលតាងឲ្យភាពខ្លាំងនៃរង្វិលនៃលំហូរ(ទិសច្រាសទ្រនិចនាឡិកាជាទិសវិជ្ជមាន) ហេតុនេះផលគុណរវាងរង្វិលនឹងវ៉ិចទ័រណរម៉ាល់ឯកតាបង្កើតបានជាកំប៉ូសង់រង្វិលលើដែន D។ ហើយការគណនាអាំងតេក្រាលនេះក្លាយជាការគណនាបរិមាណរង្វិលលើដែន D ទាំងស្រុង។
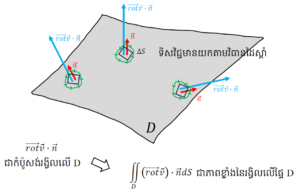
ហេតុនេះយើងអាចនិយាយបានថាតាមរយៈទ្រឹស្តីបទ Stokes ភាពខ្លាំងនៃរង្វិលតាមគន្លង Γ ជុំវិញដែន D អាចគណនាបានរយៈការគណនាបរិមាណរង្វិលសរុបនៃរង្វិលត្រង់ទីតាំងនីមួយៗ (rotv)∙n ក្នុងដែន D ទាំងស្រុង។ ភាគច្រើនគេប្រើទ្រឹស្តីនេះដើម្បីសម្រួលដល់ការគណនាអាំងតេក្រាល។ ករណីជាច្រើនអាំងតេក្រាលខ្សែមានភាពស្មុគស្មាញច្រើន តែវាត្រលប់ទៅជាងាយស្រួលវិញពេលគេបម្លែងវាទៅជាអាំងតេក្រាលផ្ទៃ។
ឧទាហរណ៍
ករណីផ្ទៃបិទ D ដូចខាងក្រោម ចំពោះដែនវ៉ិចទ័រ v ណាមួយចូរបង្ហាញថា ∫∫(rotv)∙nds = 0 ដែល n ជាវ៉ិចទ័រណារម៉ាល់ឯកតានៃផ្ទៃបិទ។
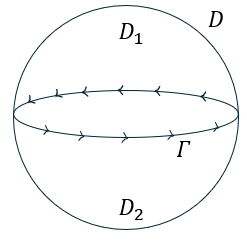
ចម្លើយគម្រូ
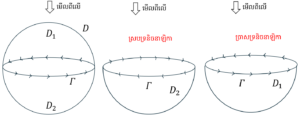
បែងចែកផ្ទៃបិទ D ដូចរូបខាងក្រោមដោយខ្សែបិទ Γ ។ តាងផ្នែកខាងលើដោយ D1 ហើយផ្នែកខាងក្រោមដោយ D2 ។ មើលពីខាងលើយើងឃើញថាគន្លង Γ នៃ D1 មានទិសស្របតាមទ្រនិចនាឡិកា ចំណែកគន្លងនៃ D2 វិញគឺ -Γ ដែលជាទិសច្រាសទ្រនិចនាឡិកា។ តាមទ្រឹស្តីបទ Stokes
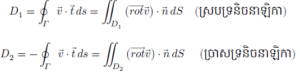
ដូចនេះគេបាន
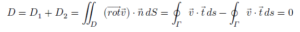
ឧទាហរណ៍
គេមានដែនវ៉ិចទ័រ v = cosyi-x(1+siny)j+0k។ តាង Γ ជាបរិមាត្ររង្វង់ដែលមានកាំ r មានផ្ចិតត្រង់គល់តម្រុយ(xoy), z = 0 ។ ចូរគណនាអាំងតេក្រាលខ្សែបិទខាងក្រោមដែល Γ ជាគន្លងវិលតាមទិសច្រាសទ្រនិចនាឡិកាបើមើលពីទិសវិជ្ជាមាននៃ z ហើយ t គឺជាវ៉ិចទ័របន្ទាត់ប៉ះឯកតានៃបរិមាត្រ Γ ។
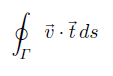
ចម្លើយគម្រូ
តាមទ្រឹស្តីបទ Stoke យើងអាចបម្លែងអាំងតេក្រាលខ្សែទៅជាអាំងតេក្រាលផ្ទៃដូចខាងក្រោម
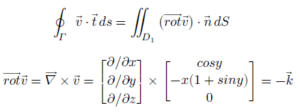
វ៉ិចទ័រណរម៉ាល់ឯកតានៃប្លង់ xoy គឺ n = k គេបាន
![]()
ដូចនេះអាំងតេក្រាលខ្សែបិទគឺ
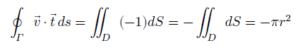
ទ្រឹស្តីបទGreenនៃប្លង់ដេក
ចំពោះដែនវ៉ិចទ័រពីរវិមាត្រ v = u(x,y)i+v(x,y)j វ៉ិចទ័រធាតុខ្សែ ds = tds វ៉ិចទ័រទីតាំង r = xi + yj គេបាន
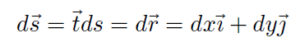
ម្យ៉ាងទៀត ធាតុផ្ទៃ dS = ndS គឺ
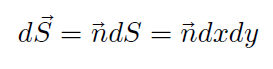
ជំនួសតម្លៃទាំងនេះទៅក្នុងទ្រឹស្តីបទ Stoke គេបាន
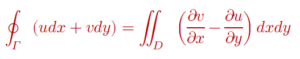
ឧទាហរណ៍
ចូរគណនាអាំងតេក្រាលខ្សែបិទខាងក្រោម។ Γ ជាគន្លងខ្សែបិទ ហើយដូចក្នុងរូបដែនកំណត់គឺ -1 ≤ x ≤ 1 , -1 ≤ y ≤ 1 ។
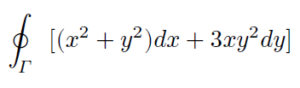
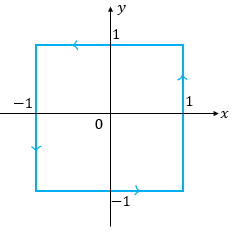
ចម្លើយគម្រូ
តាមទ្រឹស្តីបទGreen
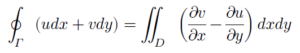
ដោយ u = x2+y2 , v = 3xy2 គេបាន
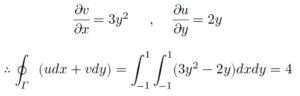
អនុវត្តទ្រឹស្តីបទ Green សម្រាប់គណនាក្រលាផ្ទៃ
តាមទ្រឹស្តីបទ Green យើងមាន
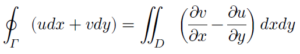
តាង v = x , u = -y យើងបាន
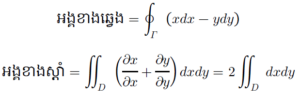
នេះមានន័យថាក្រលាផ្ទៃនៃដែន D គឺ
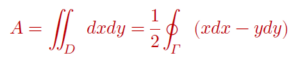
ហេតុនេះផ្ទៃដែន D អាចសរសេរជាទម្រង់អាំងតេក្រាលខ្សែលើខ្សែព្រំដែន Γ បាន។
ឧទាហរណ៍
គណនាក្រលាផ្ទៃនៃអេលីប D ដែលផ្ទៀងផ្ទាត់សមីការ
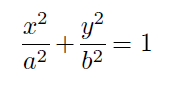
ហើយសមីការប៉ារ៉ាមែត្រ t គឺ x=accost , y =bsint ។
ចម្លើយគម្រូ
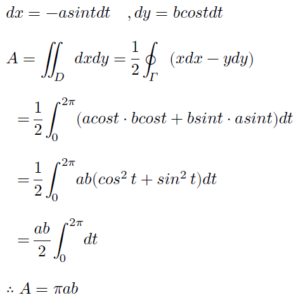
លំហាត់អនុវត្ត
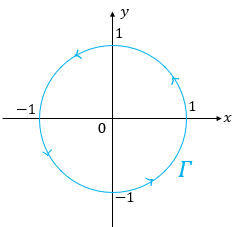
លំហាត់ទី១ តាងបរិមាត្រនៃរង្វង់ក្នុងប្លង់ yz ដែលមានកាំស្មើ 1 ដោយ Γ ។ គេមានដែនវ៉ិចទ័រ v=-yi + x2z3j+yk ។ ដោយចាត់ទុកគន្លងរង្វិល Γ ជាគន្លងវិជ្ជមានតាមទិសច្រាសទ្រនិចនាឡិកា(មើលពីទិសវិជ្ជមាននៃx) ហើយយក t ជាវ៉ិចទ័របន្ទាត់ប៉ះឯកតានៃបរិមាត្រ Γ ចូរគណនាអាំងតេក្រាលខ្សែបិទខាងក្រោម។
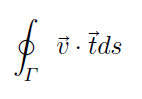
លំហាត់ទី២ ចូរគណនាអាំងតេក្រាលខ្សែបិទខាងក្រោម
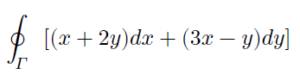
ដែលគន្លងអាំតេក្រាល Γ គឺជារង្វិលជុំវិញរង្វង់ដែលមានកាំស្មើ2 មានផ្ចិតត្រង់គល់តម្រុយ។
ចម្លើយគម្រូ
លំហាត់ទី១
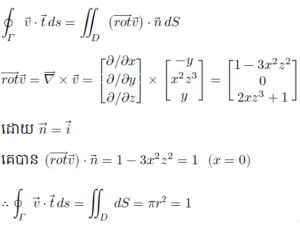
លំហាត់ទី២
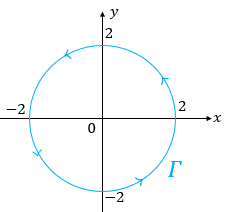
តាមទ្រឹស្តីបទGreen
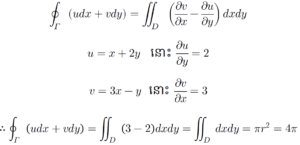
ឯកសារយោង
- 薩摩順吉,物理の数学,岩波書店,1995,pp.111-119
- Steven DiGiannurio, Peter P´erez de Corcho, Christopher Pruitt:A History of the Divergence, Green’s, and Stokes’ Theorems, https://christopherpruitt.files.wordpress.com/2015/01/a-history-of-the-divergence-greens-and-stokes-theorems.pdf
តាំងតែពីថ្នាក់ទី១០(ឆ្នាំ២០១០)រហូតដល់រៀនចប់ ក្រៅពីការសិក្សាផ្ទាល់ខ្លួន ខ្ញុំតែងតែចែករំលែកចំណេះដឹងរបស់ខ្ញុំទៅកាន់មិត្តភក្តិជានិច្ច។ ទម្លាប់នេះ ធ្វើឲ្យខ្ញុំមានគំនិតរៀបចំវែបសាយនេះឡើងដោយសង្ឃឹមថាវានឹងបានជាប្រយោជន៍សម្រាប់សាធារណជនទូទៅ។ ខ្ញុំរីករាយនឹងបន្តកិច្ចការចែករំលែកនេះតទៅទៀត។
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/
- I Uoyhttps://vijjea.com/author/uoypen/